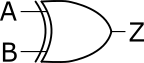
XORゲートは、入力端子のどれか1つの値が1の時だけ、出力端子から1の値を出力する基本ゲートです。一番シンプルなXORゲートは、入力端子数が2のXORゲートです(図1)。2入力XORゲートのシンボルは、2つの入力端子と1つの出力端子を持ちます。
2入力XORゲートを論理式で表したのが、(1)です。
$$Z = A \oplus B \ \ \ \ \ \text{(1)}$$
2入力XORゲートの真理値表は、\(2^2=4\)で4通りの入力の組み合わせがあります(表1)。2入力XORゲートは、入力端子のどちらか片方だけに1の値が入力される時、出力端子Zが1になります。2入力XORゲートの真理値表は、2入力ORゲートの真理値表と似ていますが、両方の入力端子が1の時の出力端子の状態が異なります。両方の入力端子の値が1の時、2入力ORゲートの出力端子の値は1になりますが、2入力XORゲートの出力端子の値は0になります。
| 入力 | 出力 | |
|---|---|---|
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
リスト1は、ハードウェア記述言語(HDL)のVerilogで記述した2入力XORゲートです。
リスト1
module xor2_mod (
input A,
input B,
output Z
);
assign Z = A ^ B;
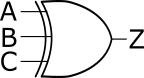
endmoduleXORゲートは、3,4,5…といったように、2つ以上の入力端子を持つ種類もあります。3入力XORゲートのシンボルは、3つの入力端子と1つの出力端子を持ちます(図2)。3入力XORゲートの論理式が(2)です。論理式からわかるように、3入力XORゲートは、2つの2入力XORゲートで実現できます。
$$Z = A \oplus B \oplus C \ \ \ \ \ \text{(2)}$$
3入力XORゲートは、入力端子が3本なので、真理値表は\(2^3=8\)の8通りの組み合わせがあります(表2)。3入力XORゲートは、1の値を持つ入力端子の数が奇数の時、出力端子Zが1になり、1の値を持つ入力端子の数が偶数の時、出力端子Zが0になります。XORゲートの入力端子数が3,4,5…と増えた場合も同様です。1の値を持つ入力端子の数が奇数の時、出力端子Zが1になります。
| 入力 | 出力 | ||
|---|---|---|---|
| A | B | C | Z |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |