JKフリップフロップは、禁止された入力値の組み合わせが存在するRSフリップフロップの不便さを解消したフリップフロップです。 回路図では図1のようなシンボルで表されます。JKフリップフロップは入力端子がJとKの2つ、出力端子が\(Q\)と\(\overline{Q}\)の2つです。\(\overline{Q}\)は\(Q\)の値を反転したものが出力されます。
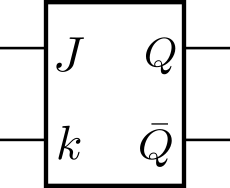
表1はJKフリップフロップの真理値表です。JKフリップフロップのJはRSフリップフロップのS、KはRSフリップフロップのRに対応します。RSフリップフロップは、RとS両方の入力が1になる組み合わせが禁止されていますが、JKフリップフロップでは、禁止されていません。JKフリップフロップでJとK両方の入力が1の場合、出力Qが現在の値から反転します。つまり、JKフリップフロップでJとK両方の入力を1に固定すると、Tフリップフロップと同じ動作になります。
| 入力 | 出力 | ||
|---|---|---|---|
| J | K | \(Q\) | \(\overline{Q}\) |
| 0 | 0 | \(Q_{PREV}\) | \(\overline{Q_{PREV}}\) |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | \(\overline{Q_{PREV}}\) | \(Q_{PREV}\) |
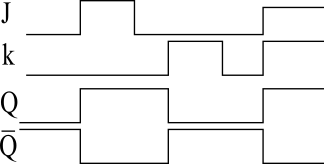
図2は図1のJKフリップフロップの動作を示すタイミングチャートです。J=1かつK=0でQ=1になります。J=0かつK=1でQ=0になります。J=1かつK=1のとき、Qは反転します。
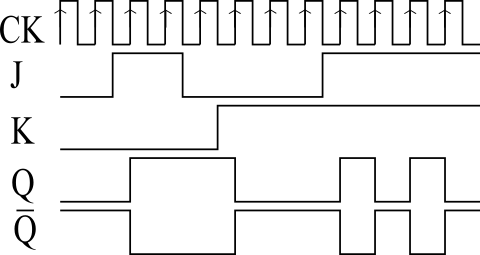
JKフリップフロップには、クロック入力端子が存在するタイプがあります(図3)。クロック入力端子が存在するタイプは、入出力信号がそのクロックに同期して動作します。立ち上がりエッジトリガタイプの場合、クロックの立ち上がりエッジで出力Qの値が変化します(図4(a))。

真理値表とカルノー図からJKフリップフロップの論理式を作成する例はこちら
