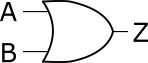
ベイチ図を使った論理式の作成例として、2入力のORゲートを取り上げます。
| 入力 | 出力 | |
|---|---|---|
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
ORゲートの真理値表からベイチ図を作成
2行2列+見出しの表を作成する
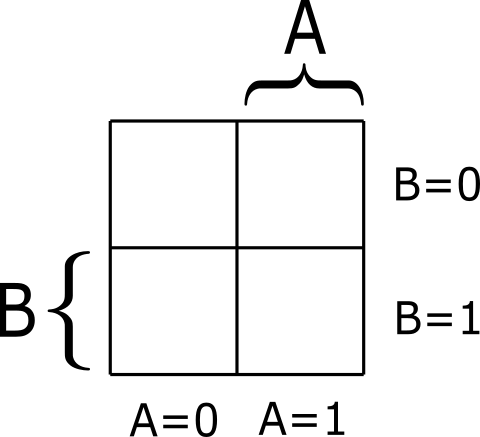
まず、ベイチ図の元になる表を作成します(図2)。ベイチ図は、回路の入力値の組み合わせの数に対応する行と列を持つ表を書き、その表のセルに回路の出力値を書きます。2入力ORゲートの入力Aと入力Bは、それぞれ0と1の2通りの値を取るので、ベイチ図は2行2列になります。
変数の割り当て
ORゲートの入力AとBを、表の行と列に割り当てます。割り当て方は自由ですが、ここでは行方向にAを、列方向にBを割り当てます(図3)。行方向のセルにA=0,1を割り当て、1を割り当てたセルの上に中かっことAを書きます。同様に列方向にB=0,1を割り当て、1を割り当てたセルの左に中かっことBを書きます。
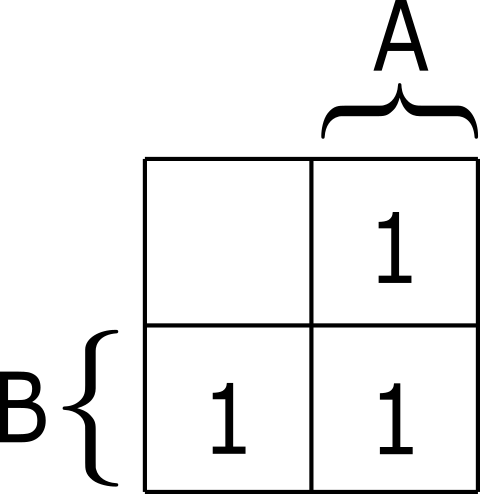
セルに値を書き込む
ORの真理値表(表1)を参考に、対応するセルに出力Zの値を書き込みます。ただし、カルノー図の場合と異なり、Z=1のセルにだけ1と書き込みます。Z=0のセルは空白のままにします。これでベイチ図は完成です(図4)。
このベイチ図のセルの値が1の3箇所に注目して、主加法標準で論理式を作成すると(1)のようになります。
$$Z = A \overline{B} + \overline{A} B + AB\ \ \ \ \ \text{(1)}$$
ORの論理式はZ=A+Bなので、(1)は冗長であり、最適化できます。
論理式の最適化
ここから、論理式(1)の最適化を行います。表のセルをグループ化し、そのグループごとに論理式を最適化します。
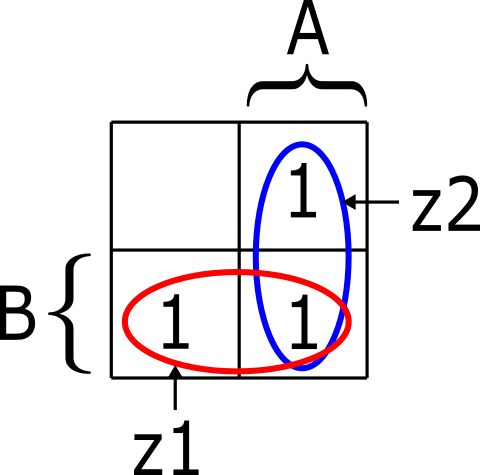
まず、図4でセルの1が連続している部分に注目し、○で囲んでグループ化します。グループ化するルールは次の通りです。
- 1のセルだけを○で囲んでグループ化する
- 囲んだセルは縦と横を2のべき乗にする
- 囲んだグループはできるだけ大きくする
- セルの囲みは、重なってもよい
- 表の上下、左右の両端はつながっている(リング状)と考える
図4にグループ化のルールを適用すると、図5のように2つの囲み(z1とz2)ができます。
まず、z1(赤い囲み)に注目します。この部分の主加法標準形の論理式が(2)です。
$$z1 = ( \overline{A} \cdot B ) + ( A \cdot B ) = (\overline{A} + A)B\ \ \ \ \ \text{(2)}$$
ブール代数より、\(\overline{A} + A=1\)です。これは、Aの値が0でも1でも結果は1ということを意味します。つまり、Aはあってもなくてもどちらでもよいので冗長です。よって、z1の囲みは(3)になります。
$$z1 = B\ \ \ \ \ \text{(3)}$$
次に、z2(青い囲み)に注目します。この部分の主加法標準形の論理式が(4)です。
$$z2 = ( A \cdot \overline{B} ) + ( A \cdot B ) = A(\overline{B} + B)\ \ \ \ \ \text{(4)}$$
ブール代数より、\(\overline{B} + B=1\)です。これは、Bの値が0でも1でも結果は1ということを意味します。つまり、Bはあってもなくてもどちらでもよいので冗長です。よって、z2の囲みは(5)になります。
$$z2 = A\ \ \ \ \ \text{(5)}$$
最後に、z1とz2からZを主加法標準形で表したのが(6)です。(6)は、本来のORゲートの論理式と一致します。
$$Z = z1 + z2 = B + A = A + B\ \ \ \ \ \text{(6)}$$