基本ゲート同士の接続関係は、回路図や論理式で表すことができます。回路図は接続関係が可視化されてわかりやすい反面、作成に手間がかかります。論理式は、回路の機能を式の形で簡潔に表すことができます。論理式は、論理関数と呼ばれることがあります。論理式では、3つの演算子か基本ゲートの代わりとして用いられます(表1)。回路図の場合と異なり、論理式では演算子の優先順位に注意が必要です。演算子の優先順位は、高い順に、否定(NOTゲート)、論理積(ANDゲート)、論理和(ORゲート)です。
| 演算子 | 機能 | 優先順位 | 使用例 |
| \(\overline{}\) | 否定 | 1 | \(\overline{A}\) |
| \(\bullet\) | 論理積 | 2 | \( A \bullet B\) |
| \( + \) | 論理話 | 3 | \( A + B\) |
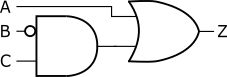
(1)は、図1の論理式です。「Bの反転とCをANDして、それをAとORしたものがZと等しい」という式です。論理積の演算子\(\bullet\)は、(2)のように省略される場合があります。
$$ Z = A + \overline{B} \bullet C \ \ \ \ \ \text{(1)} $$
$$ Z = A + \overline{B}C \ \ \ \ \ \text{(2)} $$
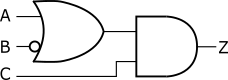
(2)の論理式は、演算子の優先順位から\(\overline{B}C \)をまず計算します。\(\overline{B}C \)より先に\(A + \overline{B}\)を計算したい場合は、(3)のようにかっこで優先順位を明示的に指定する必要があります。(3)の論理式を回路図で表したのが図2です。$$ Z = (A + \overline{B})C \ \ \ \ \ \text{(3)} $$
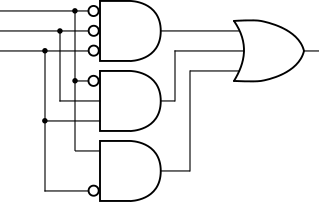
もう少し複雑な例が図3です。図3に対応する論理式が(4)です。
$$ Z= \overline{A} \ \overline{B} \ \overline{C} + \overline{A}BC + A \overline{C} \ \ \ \ \ \text{(4)} $$
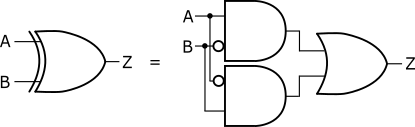
論理式の演算子は、表1以外にもXORゲートを表す\(\oplus\)があります。XORゲートは、ANDゲートとORゲートの組み合わせで実現できるので、XORゲートの演算子は必ずしも必要ではありません(図4)。XORは論理式で(5)のように表すことができます。
$$ Z= A \oplus B = A\overline{B} + \overline{A}B \ \ \ \ \ \text{(5)} $$