主加法標準形で表された論理式は、NANDゲートのみで実現できます。次の論理式をNANDゲートのみで実現する場合に必要な最小限の素子の数を求めます。
$$ Z = \overline{A} \ \overline{B} \ \overline{C} + AB \ \overline{C} + \overline{A} \ BC + A \ \overline{B} \ \overline{C} $$
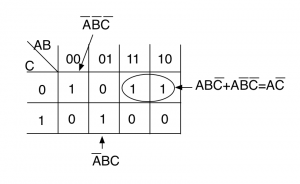
カルノー図の作成
最小限の素子を求めるために、まずカルノー図で論理の簡略化を行います。
図1: 論理式のカルノー図
カルノー図から、論理式は次のように簡略化できます。
$$ Z = \overline{A} \ \overline{B} \ \overline{C} + \overline{A} \ BC + A \ \overline{C} $$
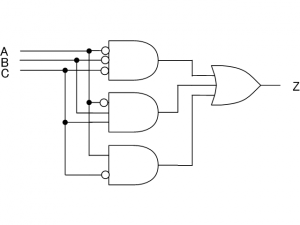
論理式の回路図を作成
簡略化を行った論理式の回路図が図2です。主加法標準形の論理式は、図2のようにANDゲートとORゲート(と入力部分のNOTゲート)で構成できます。
図2
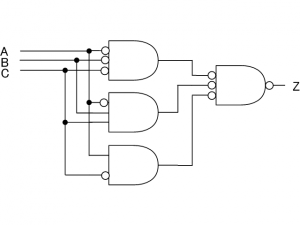
ORゲートは負論理のANDゲートと同じなので、図2の最終段を図3のように書き換えることができます。
図3
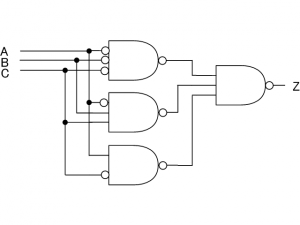
最終段の負論理のANDゲートについて、入力部分のNOTゲートはゲートを接続している線上を移動しても論理は変わらないので、図4のように移動します。
図4
NANDゲートだけで実現できました。
NANDゲートの個数
論理式を構成するNANDゲートの個数は、図4のA,B,C入力部分のNOTゲートを換算するかどうかで変わります。
入力部分のNOTゲートを無視する場合
元の論理式は4個のNANDゲートで構成できます。
入力部分のNOTゲートを無視しない場合
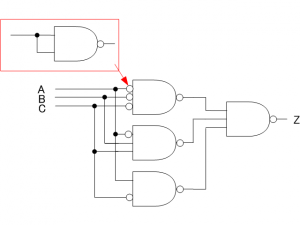
NOTゲートは、2入力のNANDゲートに置き換えることができます。図5のように、2入力NANDゲートに同じ信号を接続すると、NOTゲートと同じ機能になります。
図5
よって、図5から元の論理式は9個のNANDゲートで構成できることがわかります。