次の論理式は「A,B,Cを入力としてZを出力する論理関数」です。
$$ Z = B \overline{C} + AC + \overline{A} \ \overline{B} $$
この論理関数には双対な論理関数が存在します。
双対関数の定義は次の通りです。
$$ f_d(A,B,C) = \overline{f(\overline{A},\overline{B},\overline{C})} $$
このように、元の関数の入力を反転(0を1に、1を0に反転)し、さらに出力を反転したものが双対関数です。この定義に従って、元の論理関数に対応する双対関数を求めます。
双対関数の定義から求める
元の関数の入力と出力を反転し、ドモルガンの定理などで変形すると双対関数が得られます。
$$ Z_d = \overline{\overline{B} \ \overline{\overline{C}} + \overline{A} \ \overline{C} + \overline{\overline{A}} \ \overline{\overline{B}}}$$
$$ = \overline{\overline{B} \ C + \overline{A} \ \overline{C} + A \ B}$$
$$ = \overline{\overline{B} \ C} \bullet \overline{\overline{A} \ \overline{C}} \bullet \overline{A \ B}$$
$$ = (\overline{\overline{B}} + \overline{C})( \overline{\overline{A}} + \overline{\overline{C}})(\overline{A} + \overline{B})$$
$$ = (B + \overline{C})( A + C)(\overline{A} + \overline{B})$$
$$ = (B + \overline{C})( A \ \overline{A} + A \overline{B} + C \overline{A} + C \overline{B} )$$
$$ = (B + \overline{C})( A \overline{B} + C \overline{A} + C \overline{B} )$$
$$ = BA \overline{B} + BC \overline{A} + BC \overline{B} + \overline{C} A \overline{B} + \overline{C} C \overline{A} + \overline{C} C \overline{B}$$
$$ = BC \overline{A} + \overline{C} A \overline{B}$$
ベイチ図から双対関数を求める
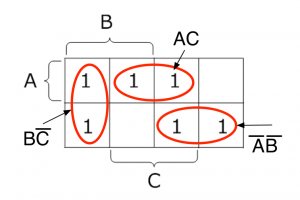
元の論理関数 \(Z = B \overline{C} + AC + \overline{A} \ \overline{B}\) からベイチ図を作成すると、次のようになります。
元の論理関数のベイチ図
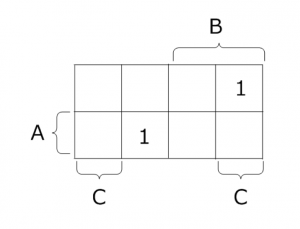
双対関数の定義に従って、ベイチ図の入力と出力を反転します(0を1に、1を0に反転)。
双対関数のベイチ図
双対関数のベイチ図から、セルが1の部分について主加法標準形で論理式を作成すると、次の論理関数が得られます。
$$ Z_d = BC \overline{A} + \overline{C} A \overline{B}$$