コンピュータ内部では、数値は32ビットや64ビットといった有限のビット数で表現されます。このため、表現できる数値の範囲や精度に制限があります。
有限のビット数を効果的に利用する目的で、整数と実数では異なる数値形式が用いられます。
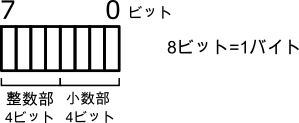
ここでは、形式の違いを比較するために、8ビット(1バイト)で整数と実数を表現します。
8ビットで区別できるのは\(2^8=256\)通りです(図1)。整数と実数を表現する形式に応じて、この256通りの区別できる箱に対して値を割り当てます。
整数
負の範囲を扱うかどうかで、有限のビット数で表現できる数の範囲が変わります。正の整数だけを扱う場合、単純に8ビットで区別できる\(2^8=256\)通りに0から255の整数を割り当てます。負の整数も扱う場合、256の範囲を正負で分割して、-128から127の整数を割り当てます(表1)。負の整数は、2の補数として表現することが一般的です。
正の整数だけを扱う形式は、C言語ではunsigned int型に対応します(8ビットの場合はunsigned char型)。また、正負の整数を扱う形式は、C言語ではint型(8ビットの場合はchar型)に対応します。
| 16進数 | 0 | \(40_{16}\) | \(7f_{16}\) | \(80_{16}\) | \(c0_{16}\) | \(ff_{16}\) |
| 正の整数だけ | 0 | 64 | 127 | 128 | 192 | 255 |
| 正負の整数(2の補数) | 0 | 64 | 127 | -128 | -64 | -1 |
実数
実数は、小数点以下の値を表現する必要があります。有限のビット数で実数を表現するには、整数を表現するビット数を減らして小数点以下の表現に割り当てるしか方法がありません。このとき、どのように整数部分と小数部分を割り当てるかで、固定小数点形式と浮動小数点形式という2つの方法があります。
固定小数点形式
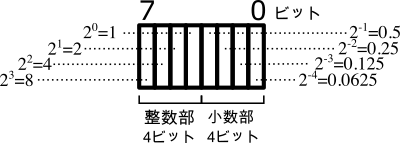
固定小数点形式では、有限のビット数のあるビット位置に小数点位置を対応させます。図2は、8ビットの上位4ビットを整数部分に、下位4ビットを小数点以下に割り当てた4.4形式の固定小数形式です。”固定”という言葉の意味は、この小数部分のビット位置が固定されていることを意味します。
4.4固定小数点形式では、整数部分は0から15までの値、また、小数部は0.0625~0.9375を表現できます。ただし、小数部は0.0625のステップでしか増減できません。図3のように、表現できる小数は0.5, 0.25, 0.125, 0.0625の組み合わせだけです。
また、固定小数点を2の補数形式として負の値も扱う場合は、表現できる正の数はこれよりも少なくなります。
4.4の固定小数点形式は、整数部分と小数部分の割り当てが均等ですが、必ずしも均等である必要はありません。整数部分と小数点以下部分のどちらの範囲を優先したいかによって割り当て方が決まります。整数部分の範囲を大きくしたい場合は、6.2といった固定小数点形式が考えられます。逆に、小数点以下の範囲を大きくしたい場合は、2.6といった固定小数点形式も考えられます。
浮動小数点形式
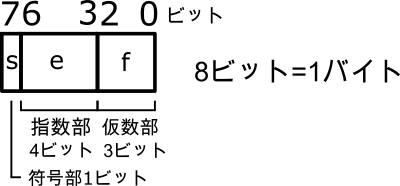
表現できる実数の範囲を精度よりも優先させた表現方法が、浮動小数点形式です。浮動小数点形式は、符号部、指数部、仮数部の3つの部分で構成されます(図4)。図4の浮動小数点形式は、(1)または(2)の式で表すことができます。
$$(-1)^s \times 2^{e-7} \times (1.f) \ \ \ \ \ \text{(1)}$$
$$(-1)^s \times 2^{e-7} \times (1+\frac{f}{2^3}) \ \ \ \ \ \text{(2)}$$
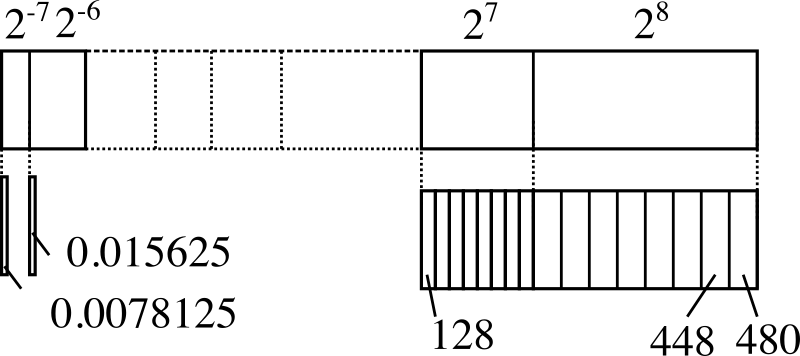
表現できる数の範囲は、+-0.0078125〜480です。ただし、この範囲のすべての実数が表現できる訳ではありません。図5は、浮動小数点の取り得る値のイメージ図です。図4の浮動小数点的式は、仮数部が3ビットなので、\(2^{-7}\)から\(2^{8}\)までの各指数の範囲で、8段階しか値を表現できません。例えば、480という値は表現できても、479という値は表現できません。480の次に小さい値は448になります。このように、浮動小数点形式では、精度を犠牲にする代わりに表現できる数値の範囲を広げてます。