浮動小数点形式は、ある有限のビット数で広い範囲の実数を扱うための仕様です。パソコンやサーバーなどのコンピュータ機器では、IEEE754と呼ばれる標準仕様が利用されています。IEEE 754は32ビットや64ビットを単位として実数を表し、それらのビット列は符号部、指数部、仮数部で構成されます。
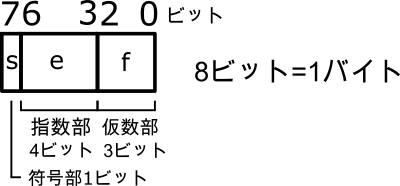
図1は、浮動小数点形式の理解を目的としてビット数を少なくした8ビットの浮動小数点形式の例です。IEEE 754と同じく符号部、指数部、仮数部で構成されます。
図1の浮動小数点形式を式で表したのが(1)です。
$$(-1)^s \times 2^{e-7} \times 1.f \ \ \ \ \ \text{(1)}$$
符号部、指数部、仮数部は次の意味を持ちます。
符号部
符号部は、その数が正(プラス)の値なのか負(マイナス)の値なのかを表します。符号部が0の時は正、1の時は負の値を表します。通常1ビットで構成されるので符号ビットとも呼ばれます。浮動小数点形式の値の正負は、符号ビットだけで判断することができます。例えば、図1の浮動小数点形式で\(80_{16}\)は最上位ビットが1なので負の数と判断できます。また、\(7F_{16}\)は最上位ビットが0なので正の数と判断できます。
指数部
指数部は、式(1)の乗数を表します。10進数の0.1を指数で表すと\(10^{-1}\)であることからもわかるように、小数点以下の値を扱うためには指数部でマイナスの値を表現する必要があります。
マイナスの値を表現する方法としては、バイアス値を用いるのが一般的です。バイアス値(オフセット値)を決めておき、eからそのバイアス値を引いた値を実際の乗数と考えます。式(1)のe-7の部分がこのバイアス値の処理です。バイアス値は、一般的に指数部のビット数が表すことができる数の半分を割り当てます。図1の場合、指数部は4ビットで0〜15を表すことができるので、7をバイアス値とします。
マイナスの値を表現する方法としては2の補数表現がありますが、指数部を2の補数表現ではなくバイアス値で表現する理由は、浮動小数点形式の値の大小比較を簡単に行うためです。指数部をバイアス値で表現すると、符号部や指数部を個別に判断することなく、浮動小数点形式のビット全体を単なる整数と考えて大小比較を行うことができます。
仮数部
仮数部は、数値の精度を表します。仮数部は、1.fの形式に正規化されます。例えば仮数部が\(0.11 \times 2^{-2}\)のときは、\(1.1 \times 2^{-3}\) と指数部を調整して仮数部の整数部を1にします。仮数部を必ず正規化することにすると、仮数部の整数部分は必ず1になることがわかっているので省略できます。式(1)の1.fという表記は、「仮数部の正規化された1は仕様から自明なので浮動小数点形式の仮数部には含まれていない」ということを意味します。この省略を行うと仮数部を1ビット増やすことができるので、浮動小数点形式の精度を向上させることができます。
浮動小数点形式の数の10進数への変換
浮動小数点形式の数は、そのビット列を見ただけでは10進数で何の値に対応するのかわかりません。ビット列を符号部、指数部、仮数部に分解して10進数に変換する必要があります。
\(36_{16}\)の例
図1の浮動小数点形式で表される8ビットの値\(36_{16}\)を10進数に変換するには、まず\(36_{16}\)を符号部、指数部、仮数部に分解します。\(36_{16}\)は2進数表記で\(00110110_{2}\)なので、符号部s=0,指数部e=\(0110_{2} = 6_{10}\),仮数部f=\(110_{2} = 6_{10}\)であることがわかります。
- 符号部s=0なので、この数は正です。
- 指数部eは、バイアス値7を引く必要があるので、実際の指数部は\(2^{6-7} = 2^{-1}\)です。
- 仮数部fは、省略されている整数部を戻して2進数で\(1.110_{2}\)です。10進数に変換すると、\(1.110_{2} = 2^{0}_{10}+2^{-1}_{10}+2^{-2}_{10} = 1_{10}+0.5_{10}+0.25_{10}=1.75\)です。
以上1.〜3.と式(1)より、\(36_{16}\)は10進数で\(1.75 \times 2^{-1} = 0.875\)であることがわかります。
\(CC_{16}\)の例
図1の浮動小数点形式で表される8ビットの値\(CC_{16}\)を10進数に変換するには、まず\(CC_{16}\)を符号部、指数部、仮数部に分解します。\(CC_{16}\)は2進数表記で\(11001100_{2}\)なので、符号部s=1,指数部e=\(1001_{2} = 9_{10}\),仮数部f=\(100_{2} = 4_{10}\)であることがわかります。
- 符号部s=1なので、この数は負です。
- 指数部eは、バイアス値7を引く必要があるので、実際の指数部は\(2^{9-7} = 2^{2}\)です。
- 仮数部fは、省略されている整数部を戻して2進数で\(1.100_{2}\)です。10進数に変換すると、\(1.100_{2} = 2^{0}_{10}+2^{-1}_{10} = 1_{10}+0.5_{10}=1.5\)です。
以上1.〜3.と式(1)より、\(CC_{16}\)は10進数で\(1.5 \times 2^{2} = 6\)であることがわかります。
指数部と仮数部のビット数の割り当てについて
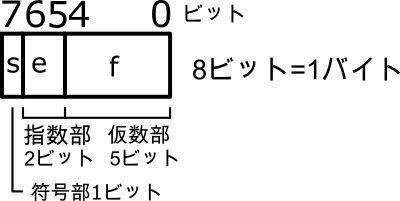
浮動小数点形式の仕様を決定するとき、指数部により多くのビット数を割り当てるか、それとも仮数部により多くのビット数を割り当てるかは、その浮動小数点形式で精度を重視するか数値範囲を重視するかで決まります。図1の浮動小数点形式は、指数部が4ビット、仮数部が3ビットです。数値の範囲は狭くてもよいので精度を重視したい場合には、指数部が2ビット、仮数部が5ビットという仕様も考えられます(図2)。指数部が2ビットの場合、バイアス値は1になります(式(2))。
$$(-1)^s \times 2^{e-1} \times 1.f \ \ \ \ \ \text{(2)}$$