ANDゲートやORゲートといった基本ゲートは、組み合わせ回路と呼ばれます。組み合わせ回路は、入力信号だけに依存して出力信号が決まります。組み合わせ回路のこの特徴は、論理ゲートの出力信号を入力信号にフィードバックする経路がなく、値を保存することができないことを意味します。値を保存する目的で使用されるのが、順序回路です。順序回路を使用することで、論理回路の過去の値(状態)を保存して参照できるようになります。順序回路には、フリップフロップとラッチと呼ばれる種類があります。
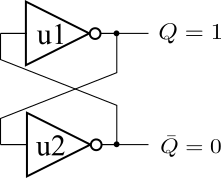
順序回路も、実は基本ゲートの組み合わせで実現されています。図1は、2つのNOTゲート(インバータ)を接続した論理回路です。インバータu1の出力がインバータu2の入力に接続され、 u2の出力がu1の入力に接続されています。u1の出力端子名を\(Q\)、u2の出力端子名を\( \overline{Q} \)とすると、\(Q\)と\( \overline{Q} \)は、0または1のどちらかの値になり、\(Q\)の値と\( \overline{Q} \)の値は反対の値になります。また、\(Q\)の値と\( \overline{Q} \)の値は、変化なく一定で保たれます。 ここでは、仮に\( Q=1 \)、\( \overline{Q}=0 \)の値になっているとします。
図1の\( Q \)と\( \overline{Q} \)の値は一定で安定しているので、値を保持する順序回路と考えることができます。次に、値を変更できるように回路を変更します。まず、図1の回路を、信号の接続状態を保ったまま\( Q \)と\( \overline{Q} \)が出力端子と見えるようにレイアウトを変更したのが図2です。
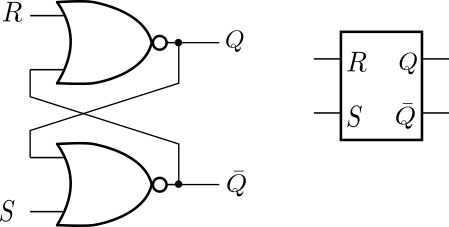
次に、\( Q \)と\( \overline{Q} \)の値を変更することができるように、図2のu1とu2のNOTゲートをNORゲートに置き換え、u1のNORゲートの片方の入力をR端子とし、u2のNORゲートの片方の入力端子をS端子としたのが図3です。このような構成にすることで、R端子とS端子を用いて\( Q \)と\( \overline{Q} \)の値を変更できるようになります。図3は、RSラッチと呼ばれる回路で、通常はR,S,\( Q \),\( \overline{Q} \)という端子を持った長方形のシンボルとして表されます。RSラッチは、RSフリップフロップと呼ばれる場合もあります。
フリップフロップには、
などの種類があります。どのフリップフロップが良く使われている(いた)かは、標準ロジックICのバリエーションの多さが参考になります。
List of 7400 series integrated circuits
DフリップフロップとJKフリップフロップは様々なバリエーションで製品化されています。実際の論理設計で使われる順序回路は、ほとんどの場合DフリップフロップとDラッチだけです。