真理値表などから作成した論理式は、最適化できる場合があります。言い方を変えると、論理式で表される入力と出力の関係を、もっと少ない論理ゲートで表現できる場合があります。このような論理式の最適化(論理圧縮)を行うために利用されるのがカルノー図やベイチ図です。
論理式を最適化することで、使用する論理ゲートを最小限にすることができます。使用する論理ゲートを減らすことができると、その論理回路を内蔵するICの物理的な大きさを小さくできる可能性があります。それによって、ICを実装するプリント基板や、プリント基板を格納する筐体の物理的な大きさを小さくできる可能性があります。
例として、次の3変数の論理式に対応するカルノー図とベイチ図を考えます。論理式の真理値表が表1です。
$$ Z = \overline{A} \ \overline{B} \ \overline{C} + \overline{A} \ \overline{B} C + AB\overline{C} + A \overline{B} \ \overline{C} + A\overline{B}C \ \ \text{(1)}$$
| A | B | C | Z |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
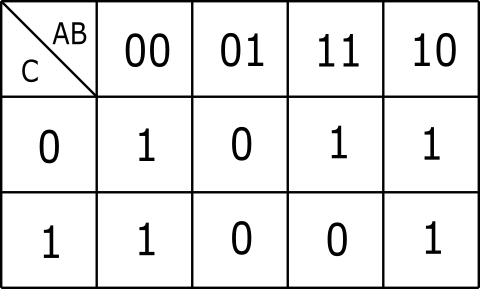
図1がカルノー図です。カルノー図は、行と列に真理値表の入力変数を振り分けた表です。真理値表の入力部分を行と列の2次元に変形した図と考えることもできます。図1では、行方向に変数AとBを、列方向に変数Cを割り当てていますが、割り当ては自由です。行と列の数は、それぞれに振り分けた変数の組み合わせの数になります。カルノー図では、表の行と列に変数値の見出しを書きます。カルノー図の各セルには、見出しに対応した真理値表の出力(Z)の値を書き込みます。
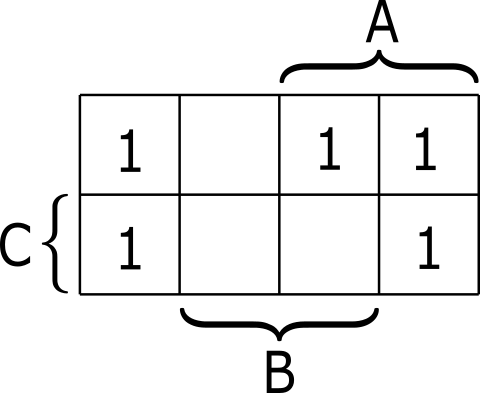
ベイチ図もカルノー図と考え方は同じです。 図2がベイチ図です。ベイチ図は変数の見出しやセル内の数字の書き方がカルノー図と異なります。ベイチ図では、行と列の見出しは、割り当てた変数が1の部分だけに書きます。また、セルに書き込む値は1の部分だけです。セルの何も書かれていない部分が0を表します。
論理設計をHDL記述と論理合成ツールで行う場合は、論理を最適化しないで、人間が読みやすく、抽象度の高い記述の方が結果的に良い論理回路が生成される場合があります。
LS標準ロジックなどのディスクリート部品を組み合わせて論理設計を行う場合には、カルノー図やベイチ図を使った論理圧縮が有効かもしれません。