順序回路は、回路への過去の入力信号などによって得られた現在の値を保持します。保持した値は、順序回路への入力信号が決められた条件に一致すると更新されます。状態遷移図を用いると、入力信号と順序回路が保持している値の変化を視覚的にわかりやすく表すことができます。
状態遷移図は、ムーア・マシンかミーリー・マシンかで表記方法が異なります。
ムーア・マシン
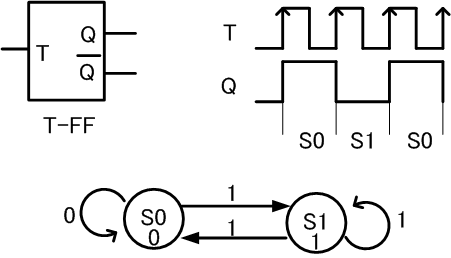
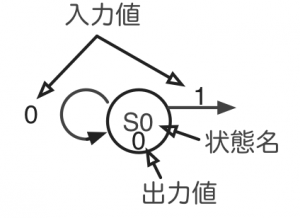
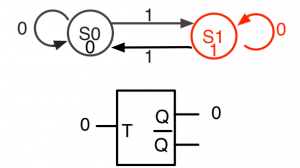
図1はTフリップフロップの動作をムーア・マシン型の状態遷移図で表したものです。ムーア・マシンでは、状態を○で表し、その中に状態名を書きます。また、状態名の下にその状態に対応した出力値を書きます(この例では、出力Qの値)。図1ではS0という状態とS1という状態があります。
- S0: Q=0に対応
- S1: Q=1に対応
矢印とその上に書かれた数字は、ある状態からある状態へ遷移する時の方向とその時の入力値を表します。矢印の始点と終点が同じ状態を指すときは、ある入力値でその状態が保持されることを意味します。
ムーア・マシンの動作
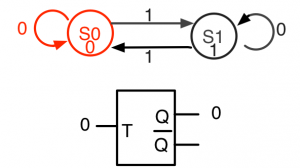
このTフリップフロップはリセット信号がないため、出力Qの初期状態は不定です(値が0なのか1なのか決まっていない)。ここでは、仮にQの初期状態を0とします。この時、Tフリップフロップの状態はS0です。入力Tが0の時、Tフリップフロップは状態S0で出力Qは0を保持します(図3-1)。
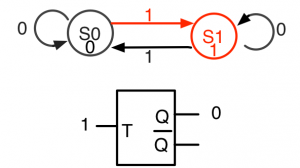
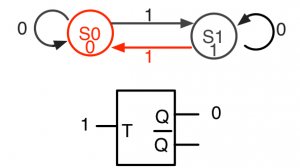
ここで、入力Tが1になると、S0を始点とする1の矢印に従って状態がS0からS1に遷移し、出力Qは1に変わります(図3-2)。
入力Tが1から0に変わっても状態S1のままです。S1を始点とする0の矢印がS1を終点としているからです。出力Qは1で変わりません(図3-3)。
次に入力Tが1になると、S1を始点とする1の矢印に従って状態がS1からS0に遷移します(図3-4)。
このように、Tフリップフロップは入力Tの値に応じて状態S0とS1の遷移を繰り返します。
ミーリー・マシン
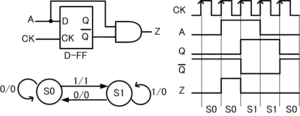
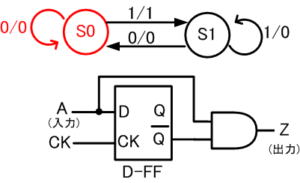
図4は信号Aの立ち上がり検出の動作をミーリー・マシン型の状態遷移図で表したものです。A信号の立ち上がり検出は、DフリップフロップとANDゲートで行います。ムーア・マシンと同様に、状態を○で表し、その中に状態名を書きます。ムーア・マシンと異なり、○の中に出力値がありません。ミーリー・マシンでは、出力値が入力値によって変化するためです。
- S0: DフリップフロップのQ=0に対応
- S1: DフリップフロップのQ=1に対応
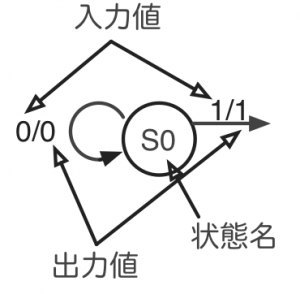
ミーリー・マシンでは、ある状態からある状態への遷移を表す矢印に2つの数字を書きます。左側に書くのが入力値、右側に書くのが出力値です。入力値と出力値はスラッシュで区切ります。ムーア・マシンと同様に、矢印の始点と終点が同じ状態を指すときは、ある入力値でその状態が保持されることを意味します。
ミーリー・マシンの動作
ここではQの初期状態を0とします。この時、Dフリップフロップの状態はS0です。入力Aが0の時、Dフリップフロップは状態S0で出力Zは0を保持します(図6-1)。
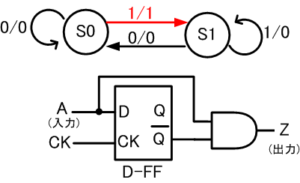
入力Aが1になると、出力Zが1に変わります。また、S0を始点とする入力1の矢印に従って状態がS1に遷移します。(図6-2)。
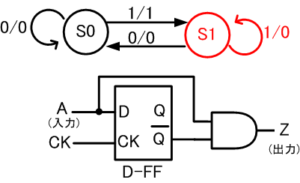
状態S1に遷移すると、出力Zは0になります。入力Aが1の間は状態S1のままです。出力Zは0のままで変わりません(図6-3)。
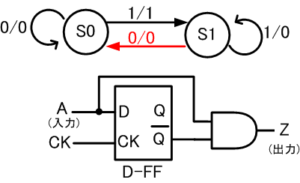
次に入力Aが0になると、S1を始点とする入力0の矢印に従って状態がS1からS0に遷移します。出力Zは0のままです(図6-4)。
実際の論理回路設計では、ブロック単位で分担して設計を行う時に「FF(フリップ・フロップ)出しにして」といったブロック間の設計ルールを決めることはありますが、ムーア・マシンやミーリ・マシンといった用語をわざわざ用いることはあまりないのではないかと思います。