パソコンやサーバーなどのコンピュータ機器では、IEEE754(IEEE Standard for Floating-Point Arithmetic )と呼ばれる浮動小数点形式(floating-point arithmetic)の標準仕様が利用されています。IEEE 754は、32ビットや64ビットを単位として実数を表します。
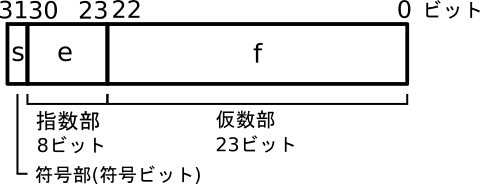
図1と図2は、IEEE754のビット構成図です。図1は32ビット単精度の構成、図2は64ビット倍精度の構成です。IEEE 754は符号部、指数部、仮数部で構成されます。(1)は図1の単精度に対応する10進数の式を表します。また、(2)は図2の倍精度に対応する10進数の式を表します。一般的に、単精度と倍精度はC言語のfloat型とdouble型に対応します。
$$(-1)^s \times 2^{e-127} \times (1.f) \ \ \ \ \ \text{(1)}$$

$$(-1)^s \times 2^{e-1023} \times (1.f) \ \ \ \ \ \text{(2)}$$
符号部s
符号部は、その数が正(プラス)の値なのか負(マイナス)の値なのかを表します。符号部が0の時は正、1の時は負の値を表します。通常1ビットで構成されるので符号ビットとも呼ばれます。
指数部e
指数部は、小数点以下の値を扱うために指数部に格納された値からバイアス値と呼ばれる固定値を引いた値が実際の指数になります。単精度のバイアス値は10進数で127、倍精度のバイアス値は1023です。図1や図2の指数部eには、このようなバイアス値が足された値が格納されます。浮動小数点同士の値を演算するときには、式(1)や(2)のように指数部からバイアス値を引く必要があります。
仮数部f
仮数部は、数値の精度を表します。仮数部は、1.fの形式に正規化されます。
正規化された仮数部の整数部分は必ず1になることがわかっているので省略できます。式(1)や式(2)の1.fという表記は、「仮数部の正規化された1は仕様から自明なので浮動小数点形式の仮数部には含まれていない」ということを意味します。例えば、式(1)で1.fが1.342のとき、単精度浮動小数点形式の仮数部fに格納されるのは、整数部分を除いた0.342だけです。浮動小数点同士の演算を行う際には、仮数部にで省略された1.0を加える必要があります。
IEEE754浮動小数点形式の16進数表記と10進数の変換
C言語のunionを利用すると、10進数の実数とそれに対応するIEEE754の16進数表記を簡単に変換することができます。次のプログラムを利用すると、10進数の1.0はIEEE754の単精度形式で\(3f800000_{16}\)であることがわかります。また、10進数の0.8は\(3f4ccccd_{16}\)であることが分かります。
$float val = 1.0
float32: 1.000000 = 3f800000 [0 7f 000000]
$float val = 0.8
float32: 0.800000 = 3f4ccccd [0 7e 4ccccd]浮動小数点形式の精度限界
単精度浮動小数点形式は、図1の仮数部fと仮数部で省略されている1のビットを足して24ビットです。24ビットで表すことができる数は \(2^{24}=16,777,216\)なので、単精度浮動小数点形式はそれ以上の数は1単位で区別することができません。
次の例は、float型に16,777,216を代入してprintfで表示した結果と、16,777,217を代入して表示した結果です。16,777,217を代入した結果は、16,777,217ではなく16,777,216と表示されてしまいます。float型で16,777,216と16,777,217は区別できないことがわかります。float型で16,777,216の次に区別可能な整数は16,777,218です。
$float val = 16777216
float32: 16777216.000000 = 4b800000 [0 97 000000]
$float val = 16777217
float32: 16777216.000000 = 4b800000 [0 97 000000]
$float val = 16777218
float32: 16777218.000000 = 4b800001 [0 97 000001]