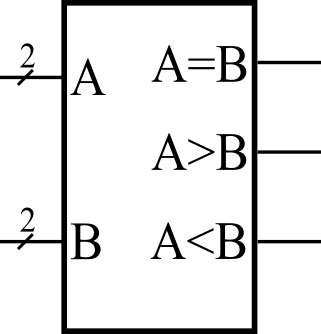
比較回路(コンパレータ)は、入力された数値を比較して、一致や大小を判定する回路です。
図1は、2つの2ビットの入力信号A,Bを比較する回路のシンボル図です。表1は、図1の比較回路の真理値表です。入力Aは2ビットで、下位ビットをA[0]で表し、上位ビットをA[1]で表します。同様に、入力Bは2ビットで、下位ビットをB[0]で表し、上位ビットをB[1]で表します。A=Bのとき出力信号A=Bが1になり、A<Bのとき出力信号A<Bが1になり、A>Bのとき出力信号A>Bが1になります。
| 入力 | 出力 | |||||
|---|---|---|---|---|---|---|
| A[1] | A[0] | B[1] | B[0] | A=B | A<B | A>B |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
出力A=B, A<B , A>Bについて、表1から主加法標準形で論理式を作成します。A=Bは、1になるAとBの組み合わせが4通りなので、論理式は(1)のようになります。
\begin{equation}
\begin{split}
A=B
= & \overline{A[1]} \cdot \overline{A[0]} \cdot \overline{B[1]} \cdot \overline{B[0]}+\\
& \ \overline{A[1]} \cdot A[0] \cdot \overline{B[1]} \cdot B[0]+\\
& \ A[1] \cdot \overline{A[0]} \cdot B[1] \cdot \overline{B[0]}+\\
& \ A[1] \cdot A[0] \cdot B[1] \cdot B[0]\ \ \ \ \ \text{(1)}
\end{split}
\end{equation}
A<Bは、1になるAとBの組み合わせが6通りなので、論理式は(2)のようになります。
\begin{equation}
\begin{split}
A<B
= & \overline{A[1]} \cdot \overline{A[0]} \cdot \overline{B[1]} \cdot B[0]+\\
& \overline{A[1]} \cdot \overline{A[0]} \cdot B[1] \cdot \overline{B[0]}+\\
& \overline{A[1]} \cdot \overline{A[0]} \cdot B[1] \cdot B[0]+\\
& \overline{A[1]} \cdot A[0] \cdot B[1] \cdot \overline{B[0]}+\\
& \overline{A[1]} \cdot A[0] \cdot B[1] \cdot B[0]+\\
& A[1] \cdot \overline{A[0]} \cdot B[1] \cdot B[0]\ \ \ \ \ \text{(2)}
\end{split}
\end{equation}
式(2)は、ブール代数の相殺則を利用して(3)のように最適化できます。
\begin{equation}
\begin{split}
A<B
= & \overline{A[1]} \cdot \overline{A[0]} \cdot \overline{B[1]} \cdot B[0]+\\
& \overline{A[1]} \cdot B[1] \cdot \overline{B[0]}+\\
& \overline{A[1] \cdot A[0]} \cdot B[1] \cdot B[0]\ \ \ \ \ \text{(3)}
\end{split}
\end{equation}
A>Bは、1になるAとBの組み合わせが6通りなので、論理式は(4)のようになります。
\begin{equation}
\begin{split}
A>B
= & \overline{A[1]} \cdot A[0] \cdot \overline{B[1]} \cdot \overline{B[0]}+\\
& A[1] \cdot \overline{A[0]} \cdot \overline{B[1]} \cdot \overline{B[0]}+\\
& A[1] \cdot \overline{A[0]} \cdot \overline{B[1]} \cdot B[0]+\\
& A[1] \cdot A[0] \cdot \overline{B[1]} \cdot \overline{B[0]}+\\
& A[1] \cdot A[0] \cdot \overline{B[1]} \cdot B[0]+\\
& A[1] \cdot A[0] \cdot B[1] \cdot \overline{B[0]}\ \ \ \ \ \text{(4)}
\end{split}
\end{equation}
式(4)は、ブール代数の相殺則を利用して(5)のように最適化できます。
\begin{equation}
\begin{split}
A>B
= & \overline{A[1]} \cdot A[0] \cdot \overline{B[1]} \cdot \overline{B[0]}+\\
&A[1] \cdot \overline{A[0]} \cdot \overline{B[1]}+\\
&A[1] \cdot A[0] \cdot \overline{B[1] \cdot B[0]}\ \ \ \ \ \text{(5)}
\end{split}
\end{equation}
HDL記述
2ビットの比較回路をVerilogで記述したのがリスト1です。3項演算子を使ってAとBをそのまま比較しています。