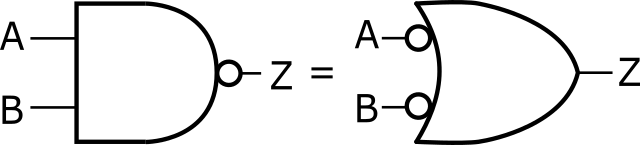論理回路を扱う場合の重要な法則です。HDLを使った論理設計では論理合成ツールが回路の最適化を行うため、設計者自身がブール代数などを使って回路の最適化を行うことはほとんどありませんが、ドモルガンの定理は、HDLを使った論理回路設計でも使用することがあります。
ドモルガンの法則は、表1の2つのルールがあります。
| No. | 法則 |
|---|---|
| 1 | 変数のANDの否定は、それぞれの否定のORに等しい |
| 2 | 変数のORの否定は、それぞれの否定のANDに等しい(番号1の双対表現) |
法則1
法則1を、AとBの2変数の論理式で具体的に表したのが、(1)です。
$$ \overline{A \bullet B} = \overline{A} + \overline{B} \ \ \ \ \ \text{(1)} $$(1)の関係を回路で表したのが図1です。NANDゲートは、入力をNOTゲートで反転したORゲートに置き換えることができることを意味します。
2入力NANDゲートの真理値表(表2)と入力を否定したORゲートの真理値表(表3)からわかるように、\(Z = \overline{A \bullet B}\)と\(Z = \overline{A} + \overline{B}\)は等価です。
| A | B | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | \(\overline{A}\) | \(\overline{B}\) | Z |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
この法則は、3変数以上の場合も成り立ちます。(2)は3変数の例です。
$$ \overline{A \bullet B \bullet C} = \overline{A} + \overline{B} + \overline{C} \ \ \ \ \ \text{(2)} $$法則2
法則2を、AとBの2変数の論理式で具体的に表したのが、(3)です。
$$ \overline{A + B} = \overline{A} \bullet \overline{B} \ \ \ \ \ \text{(3)} $$(3)の関係を回路で表したのが図2です。NORゲートは、入力をNOTゲートで反転したANDゲートに置き換えることができることを意味します。
2入力NORゲートの真理値表(表4)と入力を否定したANDゲートの真理値表(表5)からわかるように、\(Z = \overline{A +B}\)と\(Z = \overline{A} \bullet \overline{B}\)は等価です。
| A | B | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| A | B | \(\overline{A}\) | \(\overline{B}\) | Z |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
この法則は、3変数以上の場合も成り立ちます。(4)は3変数の例です。
$$ \overline{A + B + C} = \overline{A} \bullet \overline{B} \bullet \overline{C} \ \ \ \ \ \text{(4)} $$