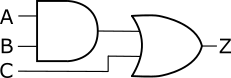
表1は、図1の論理回路に対応した真理値表です。図1の論理回路は、入力端子数がA,B,Cの3本なので、8行の真理値表になります(各入力端子は0または1の2種類の値のどちらかで、それが3本なので\(2^3=8\))。このように、真理値表は、通常、論理回路の入力端子の取り得る値の組み合わせの数だけ表の行が必要になりますが、冗長な行を省略することができる場合があります。表1は、冗長な行をまとめて省略することができる真理値表です。省略できる行は、「ある入力端子の値が、0または1のどちらであっても、出力端子の値が変わらない」行です。
| 入力 | 出力 | ||
|---|---|---|---|
| C | A | B | Z |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
図1の論理回路は、入力端子CがORゲートに接続されているので、C=1の時、出力端子Z=1です。C=1の時、入力端子AとBの値は0であっても1であって出力端子Z=1に影響しません。このような場合、表1の真理値表は、表2のようにC=1となっている下4行を1行にまとめることができます。まとめて新たに作成した行のAとBの部分には、Xと書きます。このXは、「0または1のどちらでも良い」という意味でドントケアと呼ばれます。
| 入力 | 出力 | ||
|---|---|---|---|
| C | A | B | Z |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | X | X | 1 |
表2は、もう少し省略できます。表2のC=0,A=0の行に注目すると、Bの値にかかわらずZ=0になるので、Bをドントケアで省略できます。Bをドントケアで省略した真理値表が表3です。
| 入力 | 出力 | ||
|---|---|---|---|
| C | A | B | Z |
| 0 | 0 | X | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | X | X | 1 |
ドントケアを用いて真理値表の冗長な行を省略するという作業は、真理値表を使って冗長な論理の最適化を行っていると考えることができます。例えば、真理値表から回路図や論理式を作成したい場合、表1を参照するよりも表3の真理値表を参照した方が、「C=1であれば、AとB関係なくZ=1なる」といった関係がすぐにわかるので、無駄のない回路図や論理式を作成することができます。