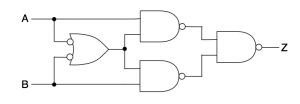
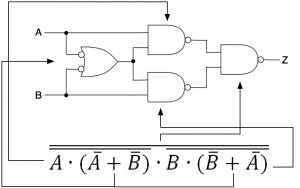
次の回路図(図1)と等価な論理式を作成します。
図1: 2入力、1出力の回路図
変換方法によって、いくつかの表現の論理式に変換できます。
- \( Z = \overline{\overline{A \bullet ( \overline{A} + \overline{B})} \bullet \overline{B \bullet ( \overline{B} + \overline{A})}} \)
- \( Z = A \bullet \overline{B} + B \bullet \overline{A} \)
- \( Z = (A + B ) \bullet (\overline{A} + \overline{B}) \)
- \( Z = A \oplus B\)
これら1.〜4.の論理式は、すべて図1と等価です。 つまり、入力A,Bに0または1の値を入れると、図1と1.～4.の式は同じZの値を出力します。
1.の論理式
回路図をそのまま論理式にすると1.になります。図の入力段のORゲートと入力の反転は、NANDゲートと等価です。
論理式と回路図の対応
2.の論理式
1.の論理式をドモルガンの定理で展開すると2.の論理式になります。
$$ Z = \overline{\overline{A \bullet ( \overline{A} + \overline{B})} \bullet \overline{B \bullet ( \overline{B} + \overline{A})}} $$
$$ = \overline{\overline{A \bullet ( \overline{A} + \overline{B})}} + \overline{\overline{B \bullet ( \overline{B} + \overline{A})}} $$
$$ = A \bullet ( \overline{A} + \overline{B}) + B \bullet ( \overline{B} + \overline{A}) $$
$$ = A \bullet \overline{A} + A \bullet \overline{B} + B \bullet \overline{B} + B \bullet \overline{A} $$
\( A \bullet \overline{A} = 0, B \bullet \overline{B} = 0 \)なので
$$ Z = A \bullet \overline{B} + B \bullet \overline{A} $$
3.の論理式
2.の論理式は主加法標準形です。つまり、\(A \bullet \overline{B}\)または\(B \bullet \overline{A}\)の場合のみZ=1になります。論理式から作成した真理値表は次のようになります。
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
この真理値表から主乗法標準形の論理式を作成すると3.になります。
$$ Z = (A + B ) \bullet (\overline{A} + \overline{B}) $$
4.の論理式
真理値表をよく見ると、これはXORゲートと同じです。
$$ Z = A \oplus B $$