エンコーダは、入力信号を数値に変換する回路です。エンコーダには、プライオリティ・エンコーダと、プライオリティなしエンコーダがあります。
エンコーダ(プライオリティなし)
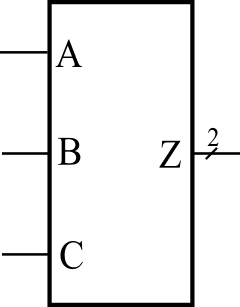
図1は、3本の1ビット入力信号A, B, Cを2進数の数値に変換する(バイナリ)エンコーダのシンボルです。表1は、図1のエンコーダの真理値表です。出力Zは2ビットで、下位ビットをZ[0]で表し、上位ビットをZ[1]で表します。プライオリティなしエンコーダは、2つ以上の入力信号が同時に1にならないという前提があります。1ビット入力A, B, Cのどれか1つが1になったとき、その入力に応じた2進数の値をZから出力します。具体的には、A=1のときZ=1(Z[1:0]=\(01_{2}\))、B=1のときZ=2(Z[1:0]=\(10_{2}\))、C=1のときZ=3(Z[1:0]=\(11_{2}\))という対応でエンコードを行ます。
| 入力 | 出力 | |||
|---|---|---|---|---|
| C | B | A | Z[1] | Z[0] |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
エンコーダの論理式
出力Zについて、表1から主加法標準形で論理式を作成します。論理式は、下位ビットZ[0]と上位ビットZ[1]でそれぞれ作成します。
Z[0]が1になるのはAまたはCが1のときです。また、前提として2つ以上の入力が1になることはないので、Z[0]の論理式は式(1)のようになります。
$$Z[0] = A + C\ \ \ \ \ \text{(1)}$$
Z[1]が1になるのはBまたはCが1のときです。また、前提として2つ以上の入力が1になることはないので、Z[1]の論理式は式(2)のようになります。
$$Z[1] = B + C\ \ \ \ \ \text{(2)}$$
プライオリティ・エンコーダ
表2は、図1がプライオリティ・エンコーダの場合の真理値表です。プライオリティ・エンコーダは、2つ以上の入力信号が1になるとき、どれか1つの入力を優先します。表2のプライオリティ・エンコーダは、C>B>Aという優先順位があります。例えば、A=1, B=1, C=1のとき、Cを優先してZ=3(Z[1:0]=\(11_{2}\))になります。Cを優先するということは、C=1のときはAとBは無視するということなので、真理値表のC=1の行のAとBはドントケアになります。
| 入力 | 出力 | |||
|---|---|---|---|---|
| C | B | A | Z[1] | Z[0] |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | x | 1 | 0 |
| 1 | x | x | 1 | 1 |
参考に、表2をドントケアを使わないで、A,B,CとZの組み合わせをすべて網羅したのが表3です。
| 入力 | 出力 | |||
|---|---|---|---|---|
| C | B | A | Z[1] | Z[0] |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
プライオリティ・エンコーダの論理式
出力Zについて表2から主加法標準形で論理式を作成します。論理式は、下位ビットZ[0]と上位ビットZ[1]でそれぞれ作成します。
表2でZ[0]が1になるのは2ヵ所です。よって、Z[0]の論理式は式(3)のようになります。
$$Z[0] = A \overline{B} \cdot \overline{C} + C\ \ \ \ \ \text{(3)}$$
Z[1]が1になるのは2ヵ所です。よって、Z[1]の論理式は式(4)のようになります。
$$Z[1] = B \cdot \overline{C} + C\ \ \ \ \ \text{(4)}$$
式(1)と(3)、(2)と(4)を比べると、プライオリティ・エンコーダの方が論理式が複雑なのがわかります。
HDL記述
3入力のプライオリティ・エンコーダをVerilogで記述したのがリスト1です。リスト1は3項演算子で記述していますが、if文やcase文で記述する場合もあります。