システムが安定とは
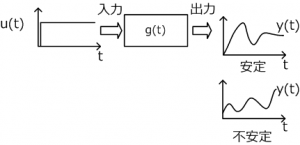
システムに入力を加えたとき、出力が発散せず収束する状態を安定と呼びます。安定したシステムでは、出力が最終的にある一定値に収束します。不安定なシステムでは、出力が一定値に収束しないで発散します。
出力の収束と発散
安定性の判断
システムの安定性には、伝達関数の極が関係します。
極と零点
伝達関数\( G(s) = \frac{GN(s)}{GD(s)} \)のとき、極と零点は次のように定義されます。
- 極: 分母多項式𝐺𝐷(𝑠)=0の根
- 零点: 分子多項式𝐺𝑁(𝑠)=0の根
極の𝐺𝐷(𝑠)=0は特性方程式と呼ばれ、システムの安定性判断に利用されます。
安定性は、伝達関数の極と次のように関係しています。
- 極の実部がすべて負であれば安定
- 極の実部が1つでも正であれば不安定
- 極の実部が0であれば安定限界
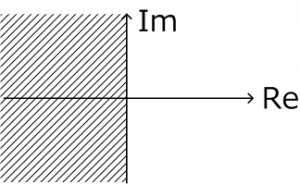
安定限界とは、収束も発散もしない(振動)状態です。安定条件は、sの複素平面上で極がすべて左半分に存在することを意味します。
安定条件
例えば、特性方程式が\( GD(s) = s^2 + 3s+ 2 = 0 \)の時、極は
$$ GD(s) = s^2 + 3s+ 2 = (s+1)(s+2) = 0 $$
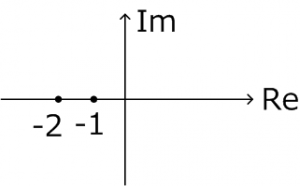
$$ s = -1, -2 $$
となります。極をsの複素平面上にプロットすると、すべて左半分に存在することから、システムは安定していることがわかります。
極は左半分に存在
2次遅れ要素の安定性
特性方程式が次の2次方程式で表されるときの安定性を考えます。
$$ GD(s) = as^2 + bs + c = 0 $$
2次方程式の解の公式から
$$ s = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$
極の2つの値を複素平面上にプロットすると次のようになります。
極と安定性の関係図
システムは、極がすべて実数軸の負の部分に存在すれば安定です。
システムの安定性は、極の実数部分と虚数部分の値に応じて次のような特徴があります。
極が実数のみの場合(虚数成分がゼロ)
振動しません。実数が正の時には振動しないで発散し、実数が負の時には振動しないで収束します。
極に虚数成分がある場合
振動を伴います。実数が正の時には振動して発散し、実数が負の時には振動して収束します。
極の実数の大きさ
極の実数が大きいほど、発散または収束が速くなります。実数が正の時には、値が大きいほど速く発散します。実数が負の時には、値が大きいほど速く収束します。