伝達関数とは
動的システム(入力の変化から出力の変化に時間がかかるシステム)は微分方程式で表されます。微分方程式で表されるシステムは、ラプラス変換を使うことで代数的に計算することができます。この時、システムを伝達関数で表します。
伝達関数は、制御システムの入力と出力の関係を表します。具体的には、入力信号のラプラス変換と出力信号のラプラス変換の比として表されます。
$$ G(s) = \frac{Y(s)}{U(s)}, Y(s) = G(s) \bullet U(s) $$
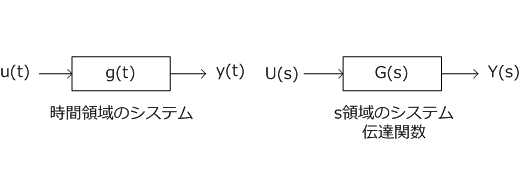
左図が入力u(t)に対して出力y(t)が出力される元のシステムです。それを伝達関数の形式で表したのが右図です。ラプラス変換後、小文字の入出力は一般的に大文字で表します。
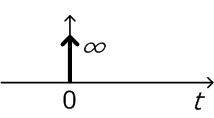
伝達関数は、「単位インパルス入力に対する出力応答のラプラス変換」とも定義されます。単位インパルス入力\( \delta(t) \)とは、「時間t=0の時に大きさが1、それ以外の時には0」という関数です。
$$ \delta(t)
= \left(
\begin{array}{ccc}
0: t \neq 0 \\
\infty : t = 0
\end{array}
\right)
$$
$$ \int^{\infty}_{-\infty} \delta(t)dt = 1 $$