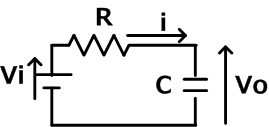
この回路はRCの積分回路です。抵抗RとコンデンサCが直接に接続されて、電源Viが接続されています。電圧viと抵抗R,コンデンサCの関係は、次の式で表されます。
$$ vi(t) = Ri(t) + \frac{1}{C}\int i(t)dt $$
この回路において、電流iとコンデンサCの両端電圧Voを求めます。
iとvoは、微分方程式を解くと最終的に次のようになります。
$$ i(t) = \frac{vi(t)}{R}e^{- \frac{t}{RC}} $$
$$ vo(t) = vi(t)(1 – e^{- \frac{t}{RC}} )$$
(eはネイピア数, e = 2.71828…)
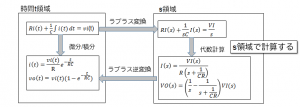
この結果は、ラプラス変換を使うと代数計算で導くことができます。
t領域->s領域への変換(ラプラス変換)
まず、時間t領域の式をラプラス変換でs 領域の式に変換します。
- i(t)はI(s)に変換
- vi(t)はVI(s)に変換
- vo(t)はVO(s)に変換
- 積分は\( \frac{1}{s} \)に変換
- 入力は単位ステップ入力\( \frac{1}{s} \)
$$ \frac{VI(s)}{s} = RI(s) + \frac{1}{sC}I(s) $$
次にこの式をI(s)の式に変形します。
$$ I(s) = \frac{VI(s)}{s(R+\frac{1}{sC})} = \frac{VI(s)}{R(s+\frac{1}{CR})}$$
また、\(VO(s)= \frac{1}{sC}I(s) \)から
$$ VO(s) = \frac{VI(s)}{sCR(s+\frac{1}{CR})} $$
ここで、ラプラス逆変換を行うために右辺を部分分数の形式に変形します。
まず右辺を部分分数で表し、その分子をA,Bとします。
$$ VO(s) = \frac{1}{CR}( \frac{A}{s} + \frac{B}{ s + \frac{1}{CR}} )VI(s) $$
\( \frac{A}{s} + \frac{B}{ s + \frac{1}{CR}} \)の部分を通分すると
$$ \frac{A(s+\frac{1}{CR})+sB}{s(s + \frac{1}{CR})} $$
この式は\( \frac{1}{s(s+\frac{1}{CR})} \)と同じになるはずなので、分子について
$$ (A+B)s = 0, \frac{A}{CR}=1 $$
よって、\( A = CR, B = -CR \)
これらから
$$ VO(s) = (\frac{1}{s} – \frac{1}{ s + \frac{1}{CR}})VI(s) $$
s領域->t領域への変換(ラプラス逆変換)
ラプラス変換表から、I(s)とVO(s)の式を逆変換すると、時間領域でのi(t)とvo(t)が求まります。
- \( \frac{1}{s+a} \)は\( e^{-at} \)に逆変換
- \( \frac{1}{s}\)は1に逆変換
$$ i(t) = \frac{vi(t)}{R}e^{- \frac{t}{RC}} $$
$$ vo(t) = vi(t)(1 – e^{- \frac{t}{RC}} )$$