ラプラス変換表（代表例の抜粋）
| t関数(時間領域) | s関数(ラプラス変換領域) |
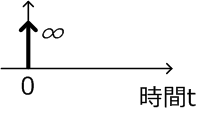
| \( \delta(t) \):単位インパルス信号 | 1 |
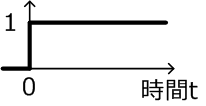
| \( u(t) \):単位ステップ信号 | \( \frac{1}{s} \) |
| \( e^{-at} \) | \( \frac{1}{s+a} \) |
| \( te^{-at} \) | \( \frac{1}{(s+a)^2} \) |
| \( t \) | \( \frac{1}{s^2} \) |
| \( t^2 \) | \( \frac{2}{s^3} \) |
単位インパルス信号と単位ステップ信号は、システムへの入力信号としてよく利用されます。
単位インパルス信号
単位ステップ信号
単位インパルス信号に対応するs関数は1です。つまり、伝達関数に単位インパルス信号を入力したものは、伝達関数そのものと同じです。
ラプラス変換の性質（代表例の抜粋）
| 性質 | t関数 | s関数 |
| 線形法則 | \( af(t) \) | \( aF(s) \) |
| 線形法則 | \( f(t) + g(t) \) | \( F(s) + G(s) \) |
| 相似法則 | \( f(at) \) | \( \frac{1}{a}F( \frac{s}{a} ) \) |
| 推移法則 | \( e^{-at}f(t) \) | \( F(s+a) \) |
| 微分法則 | \( \frac{df(t)}{dt} \) | \( sF(s) – f(0) \) |
| 積分法則 | \( \int f(t) dt \) | \( \frac{F(s)}{s} \) |
| 初期値定理 | \( \lim_{t \to 0} f(t) \) | \( \lim_{s \to \infty} sF(s) \) |
| 最終値定理 | \( \lim_{t \to \infty} f(t) \) | \( \lim_{s \to 0} sF(s) \) |
初期値定理 ： 時間領域でtを極限まで0に近づけた時のf(t) の値は、s領域でsF(s)のsを極限まで無限大に近づけることで求まります。
最終値定理 ： 時間領域でtを極限まで無限大に近づけた時の f(t) の値は、s領域でsF(s)のsを極限まで０に近づけることで求まります。