2進数の並びを多項式として表現し、情報を符号化する手法です。例えば、4ビットの2進数0011は次のように表されます。
$$ (0,0,1,1) = 0 \cdot x^3 + 0 \cdot x^2 + 1 \cdot x^1 + 1 \cdot x^0 = x + 1 $$
生成された符号語は、その符号語のビットをシフトしても符号語になるという特徴があります。巡回符号は線形符号の一種です。
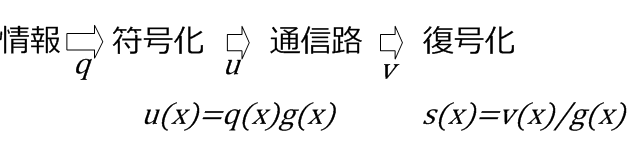
巡回符号の流れ
元の情報をqとするとき、符号語uはqと生成多項式gの演算(掛け算)で生成します。符号語uは通信路を通してvとして受信されます。受信語vを生成多項式gで割ることによって、誤り検出を行います。
符号化
kビットの情報に1ビットの誤り訂正機能を持たせるには、ハミングの限界式からnビットの符号が必要になります。これを、(n,k)線形符号と呼びます。例えば、4ビットの情報を7ビットに符号化したときは、(7,4)線形符号と呼びます。
(7,4)線形符号の例
4ビットの情報qを7ビットに符号化して符号語uを生成します。巡回符号では、次のような生成多項式gを利用します。
$$ g(x) = x^3 + x + 1 $$
例えば、4ビットの情報0011を符号化する場合、まず0011を多項式で表します。
$$ (0,0,1,1) = 0 \cdot x^3 + 0 \cdot x^2 + 1 \cdot x^1 + 1 \cdot x^0 = x + 1 = q(x) $$
次に、q(x)とg(x)の掛け算を行います。
$$ q(x) \cdot g(x) = ( x^3 + x + 1) \cdot ( x + 1)$$
$$ = ( x^4 + x^2 + x) + ( x^3 + x + 1 ) = x^4 + x^3 + x^2 + 1 = u(x)$$
符号語\( u(x) = x^4 + x^3 + x^2 + 1 \)をビット列で表すと0011101になります。
計算の途中で同じ次数の項が複数存在する場合、桁上がりはしません。例えば、\( x + x = 2x \)ではなく、\( x \oplus x = 0 \)になります。
復号
通信路から受信した受信語vは、符号化で使用した生成多項式gで誤りが発生していないかを検査します。
具体的には、通信路から受信した符号vを生成多項式gで割ります。誤りがなければ、割った余りが0になります。もともと割り切れていたはずの値が、割り切れなくなることで、誤りを検出します。