線形符号は、誤り検出訂正に使用される符号の一つです。情報の符号化と復号が効率的に行えるという特徴があります。また、符号同士を加算したものも符号になるという特徴があります。
線形符号の流れ
情報をxとするとき、符号語uはxと生成行列Gの行列演算で生成します。符号語uは通信路を通してvとして受信されます。受信語vは、検査行列Hとのマトリクス演算によって復号と誤り検出が行われます。
符号化
kビットの情報に1ビットの誤り訂正機能を持たせるには、ハミングの限界式からnビットの符号が必要になります。これを、(n,k)線形符号と呼びます。例えば、4ビットの情報を7ビットに符号化したときは、(7,4)線形符号と呼びます。
(7,4)線形符号の例
4ビットの情報を7ビットに符号化して符号語uを生成するには、4ビットの情報を1行4列のベクトルとして表し、4行7列の生成行列Gとの演算を行います。
生成行列Gは、次のような4行7列で表されます。
$$
G = \left(
\begin{array}{ccc}
1 & 0 & 0 & 0 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 & 1 & 1 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 & 1 & 1
\end{array}
\right)
$$
例えば、4ビットの情報
$$
x = \left(
\begin{array}{ccc}
1 & 0 & 0 & 0
\end{array}
\right)
$$
は、生成行列Gを使って
$$
u = \left(
\begin{array}{ccc}
1 & 0 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 0 & 0 & 0 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 & 1 & 1 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 & 1 & 1
\end{array}
\right)
$$
$$
=
\left(
\begin{array}{ccc}
1 & 0 & 0 & 0 & 1 & 1 & 1
\end{array}
\right)
$$
という符号語uになります。
ここで使用される数値や演算は、すべて2進数になります。このため、足し算に注意が必要です。行列演算中の足し算は排他的論理和(XOR)になります。具体的には、\( 1 + 1 = 1\)ではなく、\( 1 \oplus 1 = 0\)になります。
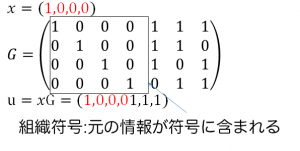
組織符号
生成行列が単位行列を含んでいる時、その生成行列で生成された符号語には、元の情報語がそのままの形で含まれます。
復号
通信路から受信した受信語vは、検査行列Hで誤りが発生していないかを検査します。誤りがなければ、受信語v = 符号語uです。
(7,4)線形符号の例
検査行列は次のような3行7列になります。
$$
H = \left(
\begin{array}{ccc}
1 & 1 & 1 & 0 & 1 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 1 & 0 & 0 & 1
\end{array}
\right)
$$
ただし、このままでは1行7列の受信語
$$
v =
\left(
\begin{array}{ccc}
1 & 0 & 0 & 0 & 1 & 1 & 1
\end{array}
\right)
$$
と行列演算ができないため、転置行列を使用します。
$$
H^{\mathrm{T}} =
\left(
\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1 & 0 \\
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right)
$$
受信語vと検査行列の行列演算の結果は次のようになります。
$$
s =
\left(
\begin{array}{ccc}
1 & 0 & 0 & 0 & 1 & 1 & 1
\end{array}
\right)
\left(
\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1 & 0 \\
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right)
=
\left(
\begin{array}{ccc}
0 & 0 & 0
\end{array}
\right)
$$
行列演算の結果sは、シンドロームと呼ばれます。sがすべて0の時には受信語vに誤りがありません。
また、組織符号で符号化された場合には、元の情報は受信語vにそのままの形で含まれています。
誤りがあった場合
シンドロームsがすべて0ではなかった場合、受信語vには誤りがあります。この時、1ビットの誤りであれば訂正が可能です。
受信語vのどのビットが誤っているかは、シンドロームsから判断できます。
具体的には、受信語vのiビット目が誤っている時、シンドロームsは検査行列\( H^{\mathrm{T}} \)のi行に一致します。
例えば、シンドロームsが
$$
s =
\left(
\begin{array}{ccc}
1 & 1 & 1
\end{array}
\right)
$$
の場合、これは検査行列\( H^{\mathrm{T}} \)の1行目に一致します。このことから、受信語vの先頭のビットが誤っていることがわかります。
誤り訂正は、受信語vの先頭ビットを反転することで行います。