加算回路は、足し算を行う論理回路です。入力された複数の値を足した結果を出力します。加算回路には、半加算回路と全加算回路という種類があります。
半加算回路
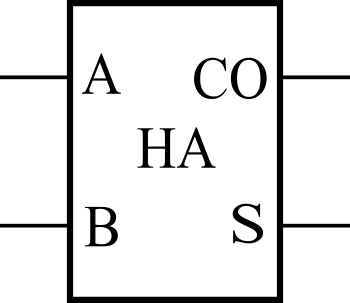
図1は、半加算回路(ハーフアダー)と呼ばれる一番簡単な1ビットの加算回路です。2つの1ビットの数AとBを足して、1ビットの結果SとCOの合わせて2ビットを出力します。
| 入力 | 出力 | ||
|---|---|---|---|
| A | B | S | CO |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
表1は、図1の回路の真理値表です。AとBという1ビットの入力が2つあるので、入力が取り得る組み合わせは \(2^2=4\)通りです。1+1の計算結果は2ですが、2進数で2を表すには\(2_{10}=10_{2}\)で2ビット必要です。出力の2ビットは、一般的に1ビットずつに分けて、下位ビットをS(サム)、上位ビットをCO(キャリー・アウト、桁上がり)で表します。
半加算回路の論理式
半加算回路を表す論理式は、出力SとCOについてそれぞれ作成します。まず、出力Sについて表1から主加法標準形で論理式を作成します。S=1となっているAとBの組み合わせは2ヵ所あるので、Sの論理式は式(1)のようになります。
$$S = \overline{A} \cdot B + A \cdot \overline{B}\ \ \ \ \ \text{(1)}$$
式(1)はXORと同じなので、Sの論理式は式(2)のようにも表せます。
$$S = A \oplus B\ \ \ \ \ \text{(2)}$$
次に、出力COについて表1から主加法標準形で論理式を作成します。CO=1となっているAとBの組み合わせは1ヵ所なので、COの論理式は式(3)のようになります。
$$CO = A \cdot B\ \ \ \ \ \text{(3)}$$
全加算回路
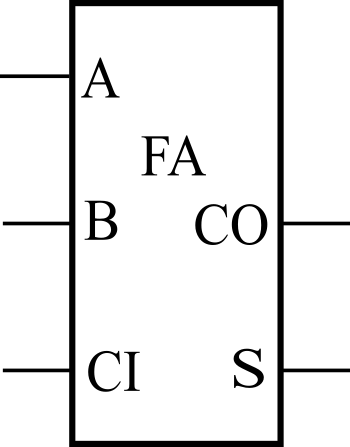
多ビット同士の加算を行う場合は、全加算回路(フルアダー)と呼ばれる回路が必要になります。全加算回路は、3入力、2出力の回路です(図2)。
全加算回路には、半加算回路には存在しないCI(キャリーイン)という入力が存在します。CIは、下の桁からの桁上がり信号を考慮して加算を行うための入力です。
全加算回路の真理値表が表2です。1ビットの入力が3つ(AとBとCI)あるので、入力が取り得る組み合わせは\(2^3 = 8\)通りです。出力は半加算器と同じで、SとCOの2ビットです。
| 入力 | 出力 | |||
|---|---|---|---|---|
| CI | A | B | S | CO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
全加算回路の論理式
半加算回路の場合と同様に、全加算回路を表す論理式を出力SとCOについてそれぞれ作成します。まず、出力Sについて表2から主加法標準形で論理式を作成します。S=1となっているA, B, CIの組み合わせは4ヵ所あるので、Sの論理式は式(1)のようになります。
\begin{equation}
\begin{split}
S
&= \overline{CI} \cdot \overline{A} \cdot B + \overline{CI} \cdot A \cdot \overline{B} + CI \cdot \overline{A} \cdot \overline{B} + CI \cdot A \cdot B\\
&= \overline{CI}(\overline{A} \cdot B + A \cdot \overline{B}) + CI(\overline{A} \cdot \overline{B} + A \cdot B)\ \ \ \ \ \text{(3)}
\end{split}
\end{equation}
式(3)は、\(\overline{A} \cdot B + A \cdot \overline{B}\)の部分がXORと同じなので、\(A \oplus B\)と置き換えることができます。また、\(\overline{A} \cdot \overline{B} + A \cdot B\)の部分はXNORと同じなので、\(\overline{A \oplus B}\)と置き換えることができます。
$$S = \overline{CI}(A \oplus B) + CI(\overline{A \oplus B})\ \ \ \ \ \text{(4)}$$
さらに、式(4)で\(A \oplus B\)部分をまとめて変数と考えると、CIと\(A \oplus B\)のXORと同じなので式(5)で表すことができます。
$$S = CI \oplus(A \oplus B)\ \ \ \ \ \text{(5)}$$
次に、出力COについて表1から主加法標準形で論理式を作成します。CO=1となっているA, B, CIの組み合わせは4ヵ所なので、COの論理式は式(6)のようになります。
\begin{equation}
\begin{split}
CO
&= \overline{CI} \cdot A \cdot B + CI \cdot \overline{A} \cdot B + CI \cdot A \cdot \overline{B} + CI \cdot A \cdot B\\
&= AB(\overline{CI}+CI) + CI(\overline{A} \cdot B + A \cdot \overline{B})\ \ \ \ \ \text{(6)}
\end{split}
\end{equation}
ここで、式(6)の\(\overline{CI}+CI\)の部分はブール代数より1になるので省略できます。また、\(\overline{A} \cdot B + A \cdot \overline{B}\)の部分はXORと同じなので、\(A \oplus B\)と置き換えることができます。よって、COは式(7)で表すことができます。
\begin{equation}
\begin{split}
CO
&= AB(\overline{CI}+CI) + CI(\overline{A} \cdot B + A \cdot \overline{B})\\
&= AB + CI(\overline{A} \cdot B + A \cdot \overline{B}) = A \cdot B + CI(A \oplus B) \ \ \ \ \ \text{(7)}
\end{split}
\end{equation}
多ビットの加算回路
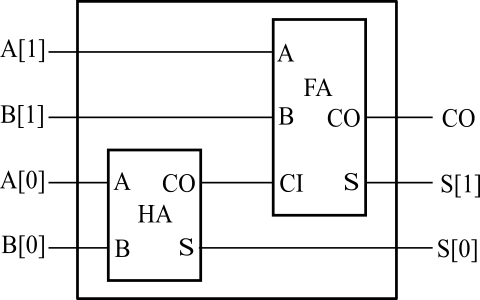
多ビットの加算を行う場合、1ビットの加算器がビット数だけ必要になります。一番簡単な2ビットの加算回路が図3です。1ビット目は、下からの桁上がりが存在しないため、半加算回路を使用します。2ビット目は全加算回路を使用します。
32ビットの加算回路の場合は、図3の1ビットの加算回路を32ビット分接続することになります。このため、回路図で表すと複雑になりますが、HDL(Verilog)では次のように簡単に記述することができます。