交流は、直流のように値が一定ではなく、刻々と変化します。このため、目的に応じて値の表し方が複数あります。
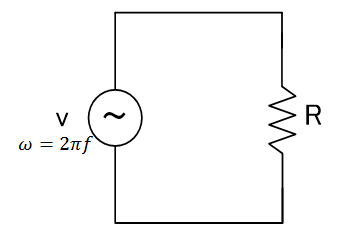
正弦波電圧の場合
回路例
波形
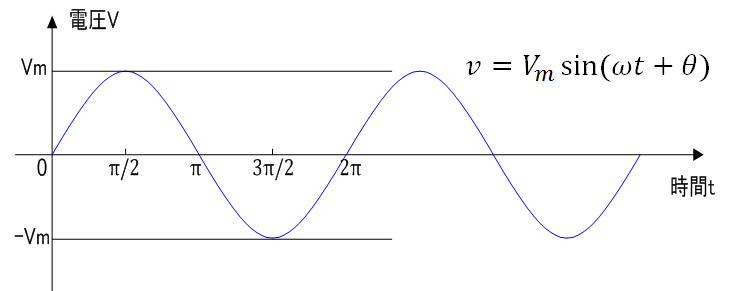
- 最大値: 正弦波のピーク値(一番大きい値) \(V_m\)
- 瞬間値: 正弦波のある瞬間の値 \(v=V_m sin(\omega t+\theta)\)(この図では\( \theta = 0\) )
- 平均値: 半周期を平均した値 \(V_a=\frac{2}{\pi}V_m\)(最大値の\(\frac{2}{\pi}\) )
- 実効値: 直流電圧の場合に同じ電力を消費する値\(V_e=\frac{1}{\sqrt{2}} V_m\)(最大値の\(\frac{1}{\sqrt{2}}\) )
シミュレーションによる具体例
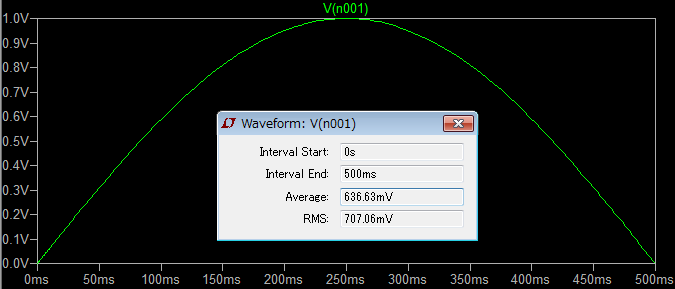
最大値1V,周波数1Hzの正弦波電圧の例です。
正弦波電圧
周波数が1Hzなので、正弦波の周期は1秒です。また、半周期は0.5秒(500mS)です。この時、電圧の平均値と実効値は次のようになります。
- 平均値: \(V_a=\frac{2}{\pi}V_m = \frac{2}{\pi}1 = \approx 636.63mV\)
- 実効値: \(V_e=\frac{1}{\sqrt{2}}V_m = \frac{1}{\sqrt{2}}1 \approx 707.06mV\)
電源電圧の半周期の波形