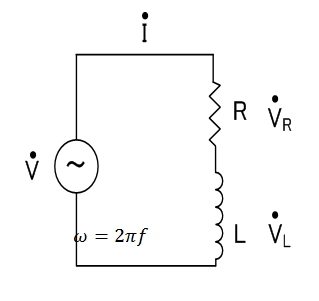
RL直列回路は、抵抗RとコイルLを直列に接続した回路です。直列接続では、RとLに同じ電流が流れます。
RL直列回路
RL回路
RL回路の電圧
\(V_R\)と\(V_L\)の関係は次のとおりです。
| 抵抗の電圧 | \(\dot{V}_R=R\dot{I}\) |
| コイルの電圧 | \(\dot{V}_L=j\omega L\dot{I}\) |
| 全体の電圧 | \(\dot{V}=\dot{V}_R+\dot{V}_L\) |
| 電圧の大きさ | \(V=\sqrt{V^2_R+V^2_L}\) |
| 位相差 | \( \theta = tan^{-1} \frac{\omega L}{R}\) |
RL回路のインピーダンス
| 電圧と電流、インピーダンスの関係 | \(\dot{V}=\dot{V}_R+\dot{V}_L=\dot{I}(R+j\omega L)\) |
| 合成インピーダンス | \(\dot{Z}=R+j\omega L\) |
| インピーダンスの大きさ | \(Z=\sqrt{R^2+(\omega L)^2}\) |
| 位相差 | \( \theta = tan^{-1} \frac{\omega L}{R}\) |
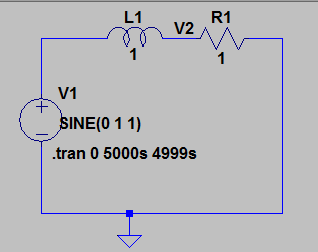
シミュレーションの例
コイルL１=1[H],抵抗R1=1[Ω]のRL直列回路に、電圧1[V], 周波数1Hzの交流電源V1を接続しています。
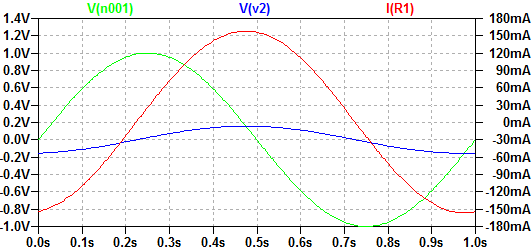
L1とR1の電圧位相差は、\(tan^{-1} \frac{\omega L}{R} = \approx 81^\circ\)です。
回路の合成インピーダンスは、\(Z=\sqrt{R^2+(\omega L)^2} = \sqrt{1^2+(2\pi)^2} \approx 6.36 \)Ωです。
RL直列回路
L1の電圧V1と、R1の電圧V2との位相差は\(81^\circ\)です。また、L1の電圧V1と電流Iの位相差も\(81^\circ\)です。V2とIは同相です。
RL回路の電流と電圧