カウンタ(counter)は、数を数える論理回路です。例えば「何回スイッチがONになったか」を数えたり、「計算処理にどの位の時間がかかったか」を計測したりする場面で利用されます。
カウンタを構成するフリップフロップ
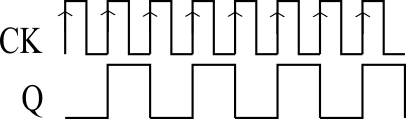
図1は、Dフリップフロップで構成した最もシンプルな1ビットのカウンタです。D入力にQ出力の反転値が入力されているので、クロックCKの立ち上がりのタイミングで出力Qが反転して0と1を繰り返します(図2)。1ビットのカウンターは、0と1を繰り返し出力することら、2進カウンタと呼ばれることがあります。また、QからクロックCKを1/2に分周したクロックを出力するので、分周回路と呼ばれることもあります。
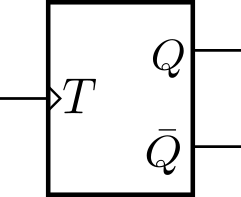
Dフリップフロップ以外にカウンタを構成するフリップフロップとしては、Tフリップフロップ(図3)やJKフリップフロップ(図4)があります。
Tフリップフロップは、T入力の変化で出力Qが反転して0と1を繰り返します。図3のTフリップフロップの内部は、Dフリップフロップを使ったカウンタ図1で構成されます。
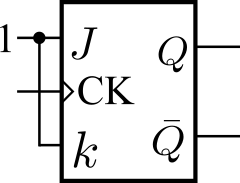
JKフリップフロップは、J=1,K=1のとき出力Qが反転する回路です。図4のようにJとKを1に固定すると、クロックCKの立ち上がりエッジでQ出力が反転して0と1を繰り返します。
2ビット以上のカウンタの構成
1ビットのカウンタは0と1しか数えることができません。それ以上の数を数えるためには、カウンタのビット数を増やす必要があります。カウンタのビット数をもう1ビット増やして2ビットにすると、そのカウンタは0~3を数えることができます。Nビットのカウンタは、0~\(2^N\)-1を数えることができます。
カウンタのビット数を増やすには、カウンタを構成するフリップフロップの数を増やす必要があります。カウンタの複数フリップフロップの接続方法には、非同期と同期の2種類があります。
非同期カウンタ
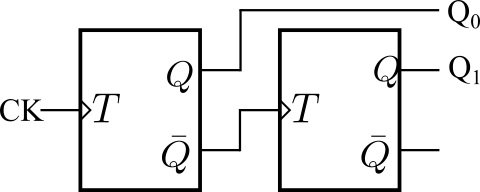
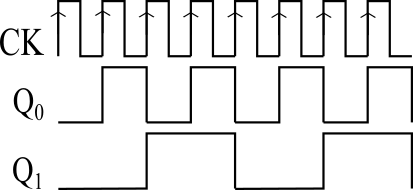
図5は、Tフリップフロップを2つ接続した2ビットのカウンタです。\(Q_{0}\)と\(Q_{1}\)で0から3をカウントします(図6)。前段Tフリップフロップの出力Qが後段Tフリップフロップの入力Tになります。このカウンタは、 カウンタを構成する2つのフリップフロップのクロック信号が異なる(同じではない=同期していない)ので、非同期カウンタと呼ばれます。
同期カウンタ
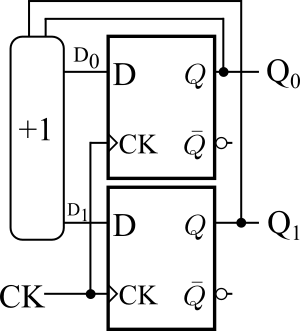
図7は、Dフリップフロップを2つ接続した2ビットのカウンタです。両方のフリップフロップに同じクロック信号が接続されていることから、同期カウンタと呼ばれます。
カウンタは、機能的には自分自身の現在の出力に1を足した結果を次のクロックタイミングでの出力する回路です。
同期カウンタでは、自分自身のQ出力に1を足した値をD入力とすること実現できます。図7の+1(1を足す)の部分の真理値表が表1です。
| 入力 | 出力 | ||
|---|---|---|---|
| Q1 | Q0 | D1 | D0 |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
表1から、D0とD1の論理式を主加法標準形で表すと、式(1)と(2)になります。
$$D_{0}=\overline{Q_{1}}\ \overline{Q_{0}}+Q_{1}\overline{Q_{0}} = \overline{Q_{0}}\ \ \ \ \ \text{(1)}$$
$$D_{1}=\overline{Q_{1}}Q_{0}+Q_{1}\overline{Q_{0}} = Q_{0} \oplus Q_{1}\ \ \ \ \ \text{(2)}$$
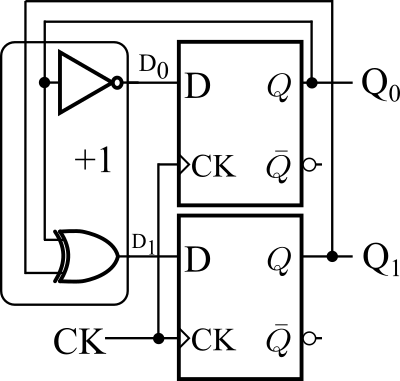
式(1)と(2)から、図7の+1の部分は、1つのNOTゲート(もしくはフリップフロップの\(\overline{Q}\)出力)と1つのXORゲートで構成されることがわかります(図8)。
同期カウンタと非同期カウンタ
非同期カウンタの方が構成がシンプルですが、実際の設計で多ビットの非同期カウンタを使うことはほどんどありません。現実世界の論理回路には信号遅延があり、またその遅延が温度や電圧によって変化します。このため、非同期カウンタは各ビット出力の値が確定するまでの時間のばらつきが多くなります。同期カウンタも、温度や電圧で信号の遅延時間が変化しますが、変化が同一クロックを起点とするのでカウンタの各ビット出力が確定するまでの遅延時間のばらつきが少なくなります。
HDL記述
32ビットの同期カウンタをVerilogで記述したのがリスト1です。HDLでは、ソフトウェアのように+1と記述するだけです。リスト1のmodule count32部分を論理合成ツールでコンパイルすると、対応する論理ゲートにマッピングされます。