Dフリップフロップの真理値表から等価な論理式を求めます。表1の\(Q_{PREV}\)は、Dフリップフロップの現在の値を表します。また、\(Q\)はCK,D,\(Q_{PREV}\)の値から決定される次のCKでの値を表します。フリップフロップはエッジトリガではないと仮定します。
真理値表とカルノー図から論理式を作成する題材としてDフリップフロップを取り上げていますが、実際の論理回路設計で基本ゲートの組み合わせによってDフリップフロップを実現することはまずありません。
| 入力 | 出力 | ||
|---|---|---|---|
| CK | D | \(Q_{PREV}\) | \(Q\) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
表1から主加法標準形で直接論理式を作成することもできますが、論理式を最適化できる可能性を検討するために、まずカルノー図を作成します。表1から作成したカルノー図が図1です。

図1のg1とg2について、それぞれ最適化を行ます。
まず、g1で囲んだ部分の論理式が(1)です。\(Q_{PREV}\)はブール代数の相殺則を適用して省略できます。
$$g1 = CK \cdot D \cdot \overline{Q_{PREV}} + CK \cdot D \cdot {Q_{PREV}} = CK \cdot D \ \ \ \ \ \text{(1)}$$
次に、g2で囲んだ部分の論理式が(2)です。Dはブール代数の相殺則を適用して省略できます。
$$g2 = \overline{CK} \cdot \overline{D} \cdot {Q_{PREV}} + \overline{CK} \cdot D \cdot {Q_{PREV}}= \overline{CK} \cdot {Q_{PREV}}\ \ \ \ \ \text{(2)}$$
よって、Dフリップフロップの出力Qの論理式は、主加法標準形で(3)になります。
$$Q = g1 + g2 = CK \cdot D + \overline{CK} \cdot {Q_{PREV}}\ \ \ \ \ \text{(3)}$$
Verilogシミュレーションで動作を確認
(3)の論理式を記述したDフリップフロップのモジュールを作成し、CKとDの値を10ナノ秒単位で切り替えてQの値を確認します。シミュレーションではQの初期値を0としています。
`timescale 1ns/1ns
// Dフリップフロップのモジュール
module d_ff (
input CK,
input D,
output reg Q,
output Qn
);
assign Qn = ~Q;
initial Q = 0; // Qの初期値は0
always @*
Q = (CK & D) | (~CK & Q);
endmodule
module top;
reg CK,D;
wire Q,Qn;
d_ff u_d_ff(.CK(CK),.D(D),.Q(Q),.Qn(Qn)); // Dフリップフロップのインスタンス
initial begin
$dumpvars; //波形出力
CK = 0;
D = 0;
#10;// 10nSごとに入力を切り替える
CK = 1;
D = 0;
#10;
CK = 0;
D = 0;
#10;
CK = 0;
D = 1;
#10;
CK = 0;
D = 0;
#10;
CK = 1;
D = 1;
#10;
CK = 0;
D = 0;
#10;
$finish;
end
endmodule結果確認
シミュレーションで出力される波形をを確認すると、CK=1でDの値を取り込み、Qとして出力していることがわかります。
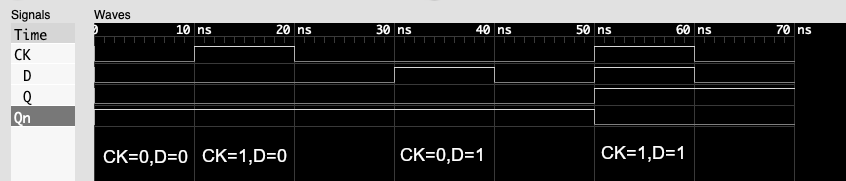
module d_ffは論理式の動作を確認することを目的としたシミュレーション用であり、実際のFPGAやASIC向けの論理設計でこのような記述のDフロップフロップを実装することはまずありません。
