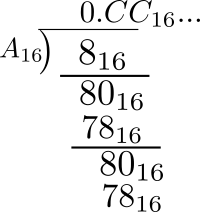循環小数は、小数点以下である数のパターンが周期的に無限に続く小数です。例えば、10進数で1/3を計算すると、小数点以下に3が無限に続きます。
$$1/3 = 0.33333….$$
別の例としては、1/11も循環小数です。09というパターンが無限に続きます。
$$1/11 = 0.090909090…..$$
循環小数の無限に続く小数点以下の表記方法にはいくつかの種類がありますが、ここでは循環する数の範囲の最初と最後にドットを付けることで表します。
この表記法では、1/3は\(1/3=0.33333….= 0.\dot{3} \)と表します。
また、\(1/11 = 0.090909090….. = 0.\dot{0}\dot{9} \)と表します。
循環小数と基数
基数が変わると、循環小数になる数があります。
例えば、10進数の0.8は循環小数ではありませんが、16進数で表すと\(0.CCC{16}….. = 0.\dot{C} \)と循環小数になります。コンピュータの演算の精度は32ビットや64ビットと有限であるため、10進数の0.8は\(0.\dot{C} \)の近似値が使われることになります。
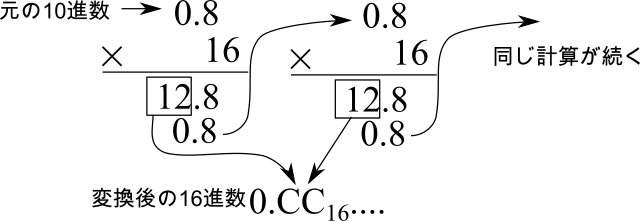
次に、実際に10進数の0.8を16進数に変換してみます。
10進数の0.8を16進数に変換する
10進数の小数を16進数に変換するには、元の10進数の小数部に変換先の基数16を掛け、その結果の小数部分が0になるまで16の掛け算を繰り返します。図1のように、掛け算結果の整数部を順に並べると、10進数の0.8は、16進数では\(0.\dot{C} \)と循環小数になることがわかります。
別な変換方法として、
10進数の0.8を分数の形\( \frac{8_{10}}{10_{10}} \)にして、この分子と分母を16進数で\(\frac{8_{16}}{A_{16}}\)と表してから筆算で割り算したのが図2です。10進数の.8は、16進数では\(0.\dot{C} \)と循環小数になることがわかります。
無限等比数列の和の公式を応用した変換
等比数列と無限等比数列の和の公式
等比級数は、初項がa, 公比がrのとき
$$a,ar,ar^2,ar^3,…$$
となる等比数列の各項を加えた式です。
$$a+ar+ar^2+ar^3+…$$
等比数列の各項を無限に足し合わせるとき、次の式が成り立ちます。
初項がa, 公比がrの無限等比級数の和は\( \frac{a}{1 – r} \)
ただし、-1 < r < 1
例えば、初項が0.2, 公比が0.1の無限等比級数の和は
\( \frac{0.2}{1 – 0.1} = \frac{0.2}{0.9} = 0.2222… = 0. \dot{2} \)となります。
基数変換への応用
循環小数\( 0. \dot{2} \)の例を16進数の場合に置き換えると、
16進数の循環小数\( 0. \dot{X} \)は、初項が\( 0.X_{16}\)、公比が\( 0.1_{16}\)の無限等比級数の和で表すことができます。また、無現等比級数の和の式から\( 0. \dot{X} \)は\( \frac{X_{16}}{f_{16}} \)と等しいことがわかります。
$$ 0. \dot{X}_{16} = \frac{0.X_{16}}{1-0.1_{16}} = \frac{ \frac{X_{16}}{10_{16}}}{ \frac{10_{16}}{10_{16}}-\frac{1_{16}}{10_{16}}} = \frac{ \frac{X_{16}}{10_{16}}}{ \frac{f_{16}}{10_{16}}} = \frac{X_{16}}{f_{16}} $$
この\(0. \dot{X} = \frac{X_{16}}{f_{16}}\)という式を利用すると、10進数に対応する16進数の循環小数\(0. \dot{X}_{16}\)を求めることができます。
0.8の16進数変換に適用する
まず、10進数の0.8を分数の形で表します。
$$ 0.8_{10} = \frac{8_{10}}{10_{10}} = \frac{4_{10}}{5_{10}} $$
\(0. \dot{X} = \frac{X_{16}}{f_{16}}\)という関係があるので、\(\frac{4_{10}}{5_{10}} \)の分母が\(f_{16}=15_{10}\)になるように分母と分子に3を掛けて調整します。
$$ \frac{4}{5} = \frac{12}{15} = \frac{C_{16}}{f_{16}} $$
よって
$$ \frac{C_{16}}{f_{16}} = 0. \dot{C}_{16} $$
となります。
2進数で表す場合
16進数の循環小数\(0. \dot{C}_{16}\)を2進数で表すときは、\( C_{16} = 1100_{2} \)なので次のようになります。
$$ 0. \dot{C}_{16} = 0. \dot{1}10\dot{0} $$