具体的な例として、10進数の\( 11.4375_{10} \)を4進数に変換します。整数部と小数部を別々に変換し、2つの結果を結合します。
基数を明確にするために、数値の最後に下付き文字で基数を付加します。例えば、10進数の1という数値は\( 1_{10} \)と表記します。2進数の1という数値は\( 1_{2} \)と表記します。16進数の1という数値は\( 1_{16} \)と表記します。
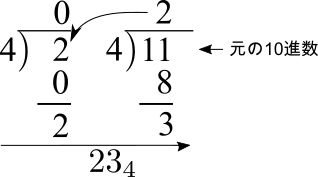
整数部
図1のように、元の10進数の整数部を変換先の基数4で割り、その商が0になるまで4で商を繰り返し割ります。割り算の余りを順に並べると、10進数の\( 11_{10} \)は、8進数の\( 23_{4} \)に対応することがわかります。
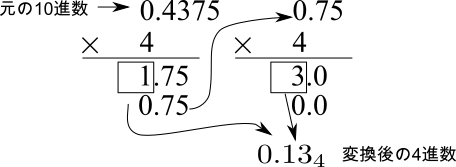
小数部
図2のように、元の10進数の小数部に変換先の基数4を掛け、その結果の小数部分が0になるまで4の掛け算を繰り返します。掛け算結果の整数部を順に並べると、10進数の\( .4375_{10} \)は、4進数の\( .13_{4} \)に対応することがわかります。
整数部と小数部の変換結果の結合
整数部と小数部の変換結果から、10進数の\( 11.4375_{10} \)は、4進数の\( 23.13_{4} \)に対応することがわかります。
検算
4進数\( 23.13_{4} \)を10進数に変換して、結果が\(11.4375_{10} \)になるか確認します。
\begin{equation}
\begin{split}
23.13_{4}
&= 2_{4} \times 4^1_{10} + 3_{4} \times 4^0_{10} + 1_{4} \times 4^{-1}_{10} + 3_{4} \times 4^{-2}_{10}\\
&= 2_{10} \times 4_{10} + 3_{10} \times 1_{10} + 1_{4} \times \frac{1}{4} + 3_{10} \times \frac{1}{16}\\
&= 8_{10} + 3_{10} + 0.25_{10} + 0.1875_{10}\\
&= 11.4375_{10}
\end{split}
\end{equation}