Dフリップフロップは、信号の値を保存する目的で最も良く利用される論理回路です。 回路図では図1のようなシンボルで表され、入力端子としてDとCK(クロック)、出力端子として\(Q\)と\(\overline{Q}\)を持ちます。CK端子に付けられている”>”記号は、フリップフロップがクロック変化のエッジでDの値を取り込むことを意味します(エッジトリガ)。Dの値を取り込むクロックのエッジは、立ち上がりまたは立ち下がりのタイプがあります。Dフリップフロップが立ち下がりエッジタイプの場合、シンボルのCK端子にNOTゲート(インバータ)を表す○が付きます。CK端子に○がない場合、立ち上がりエッジタイプを意味します。
立ち上がりエッジタイプのDフリップフロップの真理値表が表1です。CKの立ち上がりエッジのタイミングでDの値を取り込み、\(Q\)から出力します。\(\overline{Q}\)は\(Q\)の反転値が出力されます。CKの立ち上がり以外のタイミングでは、過去に取り込んだ値\(Q_{PREV}\)を保持します。
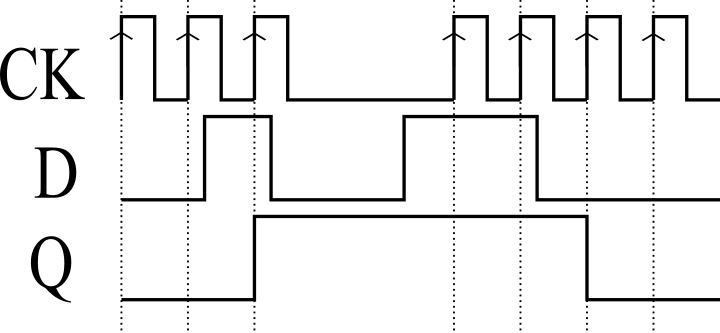
図2は立ち上がりエッジタイプのDフリップフロップの動作を示すタイミングチャートです。CKの立ち上がりでDの値を取り込み、その値を\(Q\)と\(\overline{Q}\)から出力します。CKの立ち上がり以外のタイミングでDの値をフリップフロップに取り込むことはありません。
| 入力 | 出力 | ||
|---|---|---|---|
| CK | D | \(Q\) | \(\overline{Q}\) |
| 0 | X | \(Q_{PREV}\) | \(\overline{Q_{PREV}}\) |
| ↑ | 0 | 0 | 1 |
| ↑ | 1 | 1 | 0 |
立ち下がりエッジタイプのDフリップフロップの真理値表が表2です。CKの立ち下がりエッジのタイミングでDの値を取り込み、\(Q\)から出力します。\(\overline{Q}\)は\(Q\)の反転値が出力されます。CKの立ち下がり以外のタイミングでは、過去に取り込んだ値\(Q_{PREV}\)を保持します。
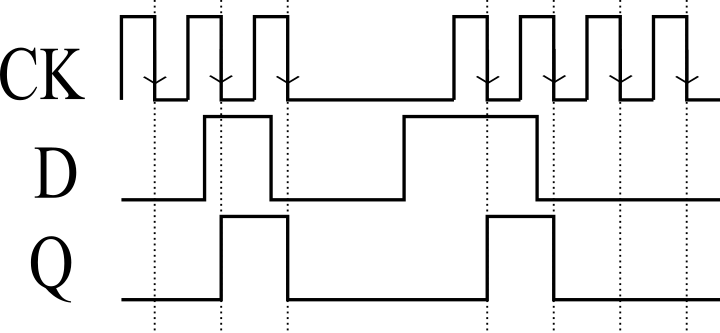
図3は立ち下がりエッジタイプのDフリップフロップの動作を示すタイミングチャートです。CKの立ち下がりでDの値を取り込み、その値を\(Q\)と\(\overline{Q}\)から出力します。CKの立ち下がり以外のタイミングでDの値をフリップフロップに取り込むことはありません。
| 入力 | 出力 | ||
|---|---|---|---|
| CK | D | \(Q\) | \(\overline{Q}\) |
| 0 | X | \(Q_{PREV}\) | \(\overline{Q_{PREV}}\) |
| ↓ | 0 | 0 | 1 |
| ↓ | 1 | 1 | 0 |
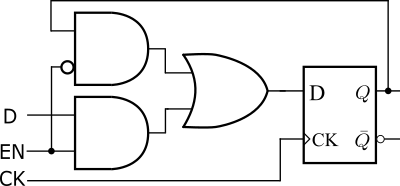
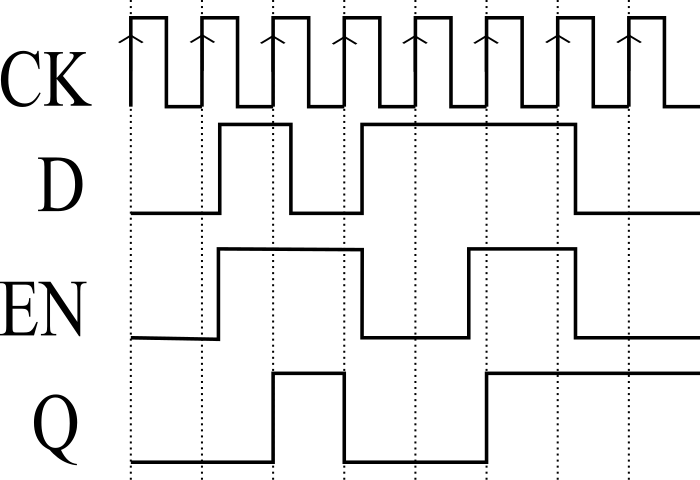
DフリッップフロップはクロックのエッジでDの値を取り込むので、あるタイミングのDの値を保持し続けるためには、クロックを止めるかイネーブル付きDフリップフロップを使う必要があります。イネーブル付きDフリップフロップは、Dフリップフロップと組み合わせ回路で実現されます(図4)。イネーブル付きDフリップフロップでは、常にクロックが供給されていてもENの制御で特定のタイミングのDの値を保持することができます。図5はイネーブル付きDフリップフロップの動作を示すタイミングチャートです。イネーブル付きDフリップフロップは、EN=1のときにDの値をDフリップフロップに取り込み、EN=0ときはDの値をDフリップフロップに取り込まず、過去の値を保持します。
真理値表とカルノー図からDフリップフロップの論理式を作成する例はこちら