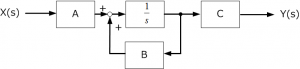
次のブロック図で表される1次元の制御システムの伝達関数\( G(s) = \frac{Y(s)}{X(s)} \)とシステムの安定条件を求めます。
1次元制御システム
手順は次のとおりです。
1. ブロック図を結合してシステムの伝達関数を求める
2. 特性方程式の極を求める
1. ブロック図を結合してシステムの伝達関数を求める
まず、フィードバック部分を結合します。プラス符号のフィードバック結合は
\( G(s) = \frac{G1(s)}{1-G1(s)G2(s)} \)より
$$ G'(s) = \frac{\frac{1}{s}}{1-\frac{1}{s}B} = \frac{1}{s-B} $$
フィードバック部分の結合
前後の直列部分のブロックを結合すると、伝達関数は次のようになります。
$$ G(s) = AG'(s)C = \frac{AC}{s-B} $$
2. 特性方程式の極を求める
伝達関数の特性方程式は\( GD(s) = s – B = 0\)
よって、極は\( s = B \)
システムが安定であるためには、特性方程式の極が負の値になる必要があるので
$$ B < 0 $$