浮動小数点形式の数は正規化と呼ばれる処理が行われます。正規化は、 浮動小数点形式の仮数部が1.xの形になるように仮数部と指数部の値を調整する処理です。正規化の処理は、浮動小数点形式の加減算や剰余算の演算などを行った後で必要になります。
正規化の例として、4194305.0-4194304.5をIEEE 754単精度形式で計算します。
4194305-4194304.5の計算
単精度形式の表現
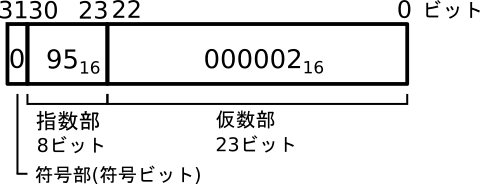
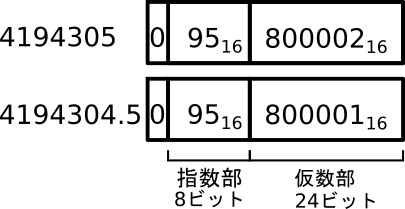
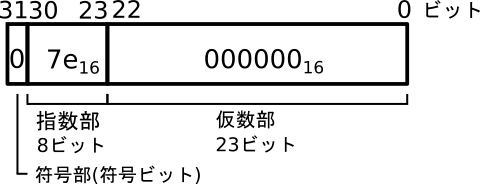
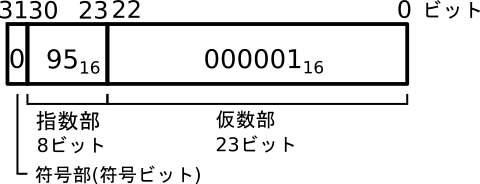
4194305をIEEE754単精度形式で表すと、符号部s=0, 指数部e= \(95_{16}\),仮数数部f=\(000002_{16}\)になります(図1)。同様に、4194304.5は符号部s=0, 指数部e=\(95_{16}\),仮数数部f=\(000001_{16}\)になります(図2)。
減算処理
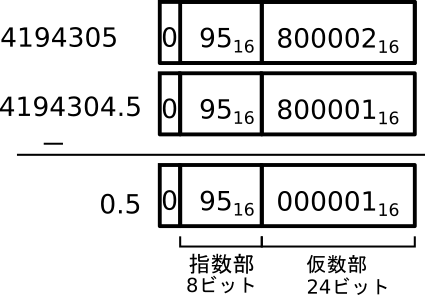
まず、4194305-4194304.5を行うためには、図1と図2の仮数部に、IEEE754で省略されている1を追加して、仮数部を24ビットとします(図3) 。
浮動小数点形式同士の数の加減算は、指数部の乗数を一致させてから仮数部の演算を行う必要がありますが、今回は指数部の乗数が同じなのでそのままの状態で仮数部の引き算を行うことができます。実際に引き算を行った結果が図4です。結果は、0.5になります。
正規化
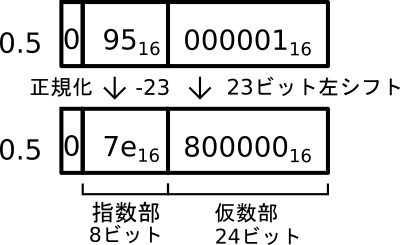
図4の結果は、仮数部が正規化されていません。正規化するには、仮数部の24ビット目を1にする必要があります。まず、図4の結果の仮数部を23ビット左シフトすると、仮数部の24ビット目が1になります。次に、指数部を調整します。仮数部を23ビット左シフトするということは、0.5を \(2^{23}\)倍したことになるので、指数部を\(1/2^{23}\)倍します。具体的には、指数部の\(95_{16}=149_{10}\)から23を引いて\(149_{10}-23_{10}=126_{10}=7e_{16}\)とします。
最後に、仮数部の24ビット目の1を省略すると、正規化されたIEEE754形式の0.5になります。
正規化しないとどうなるか
図4の正規化前の仮数部で0.5を表すビットは、仮数部の最下位ビットの1です。これは、仮数部が区別できる最小の数は0.5であるということを意味します。このため、正規化を行わないと次に行う計算で0.5より小さい値の計算が正確に行えなくなります。例えば、次に0.5から0.25を引いたとしても、結果が0.25にはなりません。正規化を行うと、仮数部に23ビット分の精度が確保できるので、 次に0.5から0.25を引いても正しい結果を得ることができるようになります。