ベクトル表記法は、交流回路の電圧、電流、インピーダンスなどを表します。コイルやコンデンサを含む交流回路では、電流と電圧に位相のずれがあります。ベクトル表記法を使うと、電流と電圧の関係を視覚的にわかりやすく表現できます。
ベクトル表記法について
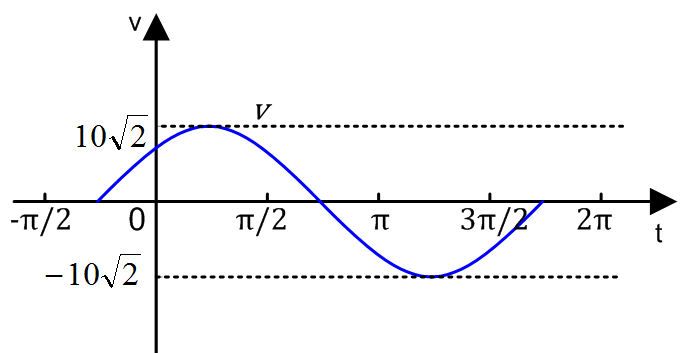
ベクトル表記法は、実効値で表します\(\dot{V}, \dot{I}, \dot{Z}\)。ベクトル表記法には、極座標表記と直交座標表記があります。次の電圧波形を、2通りのベクトル表記法で表します。
交流電圧
極座標表記
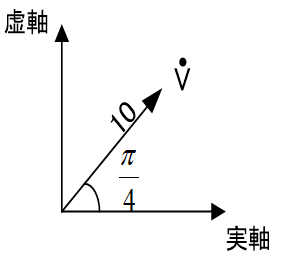
極座標表記
ベクトルの長さ10と角度(偏角)\(\frac{\pi}{4}\)で値を表します。
直交座標表記
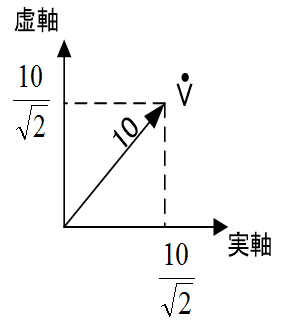
直交座標表記
ベクトルの長さ10と実数軸の値と虚数軸の値を表します。
極座標表記と直交座標表記の関係
極座標表記と直交座標表記には次の関係があります。
| 瞬間値表記 | \(v=10\sqrt{2}sin(\omega t + \frac{\pi}{4})\) |
| 極座標表記 | \(\dot{V}=10\angle \frac{\pi}{4}\) |
| 直交座標表記 | \(\dot{V}=\frac{10}{\sqrt{2}}+j\frac{10}{\sqrt{2}}\) |
ベクトル表記法の例
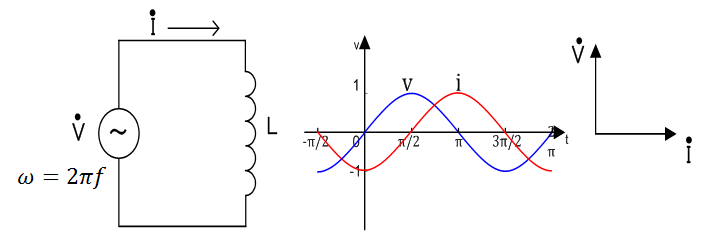
コイル
コイルの電源・電流のベクトル表記
電圧\(\dot{V}\)は、電流\(\dot{I}\)より90°進みます。
電流\(\dot{I}\)は、電圧\(\dot{V}\)より90°遅れます。
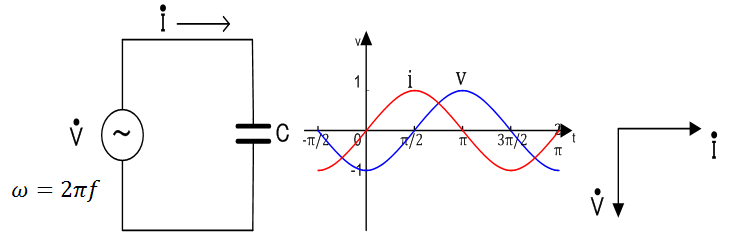
コンデンサ
コンデンサの電圧・電流のベクトル表記
電圧\(\dot{V}\)は、電流\(\dot{I}\)より90°遅れます。
電流\(\dot{I}\)は、電圧\(\dot{V}\)より90°進みます。