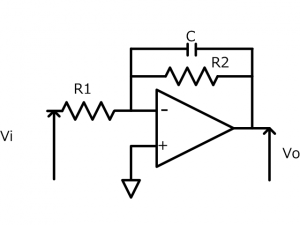
図の回路について、伝達関数 \( G(s)= \frac{Vo}{Vi} \) を求めます。
積分回路
手順は次の通りです。
1. 回路の種類を判別
2. コンデンサのラプラス変換
3. インピーダンスを求める
4. 増幅率の式にあてはめる
回路の種類を判別
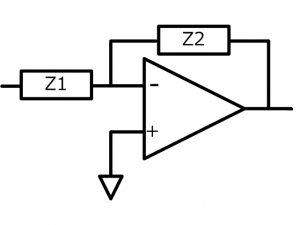
図の回路はオペアンプを使った積分回路です。また、回路のR1をZ1、CとR2の合成インピーダンスをZ2とおくと、この構成は反転増幅回路です。
コンデンサのラプラス変換
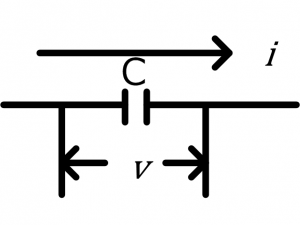
コンデンサを流れる電流をiとすると、iは次の式で表されます。
$$ C\frac{dv}{dt} = i $$
ラプラス変換の微分法則を利用して時間領域の関数をs領域の関数に変換します。ラプラス変換の微分法則は次のとおりです。
$$ \frac{df(t)}{dt} = sF(s) – f(0) $$
これを利用してコンデンサの電流の式\(C\frac{dv}{dt} = i \)の両辺をラプラス変換すると
$$ CsV = I (だだしf(0)=Vの初期値は0とする)$$
よって、コンデンサのリアクタンスは
$$ \frac{V}{I} = \frac{1}{Cs} $$
コンデンサに流れる電流
インピーダンスを求める
Z2のインピーダンスを計算すると、オームの法則から
$$ \frac{1}{Z2} = \frac{1}{R2} + \frac{1}{\frac{1}{Cs}} = \frac{1}{R2} + Cs = \frac{1+R2Cs}{R2} $$
$$ Z2 = \frac{R2}{1+R2Cs} $$
また、
$$ Z1 = R1 $$
増幅率の式にあてはめる
伝達関数 \( G(s)= \frac{Vo}{Vi} \) と反転増幅器の増幅率式\( Av= -\frac{Z2}{Z1} \)から
$$ G(s)= -\frac{Z2}{Z1} = -\frac{1}{R1} \frac{R2}{1+R2Cs} = – \frac{R2}{R1} \frac{1}{1+R2Cs} $$