次の3変数の論理式からベイチ図を作成し、論理式の簡略化(論理圧縮)を行います。
$$ Z = \overline{A} \ \overline{B} \ \overline{C} + \overline{A} \ \overline{B} C + AB\overline{C} + A \overline{B} \ \overline{C} + A\overline{B}C \ \ \ \ \ \text{(1)}$$
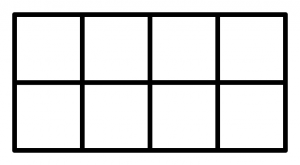
2行4列の表を作成する
3変数のうち、2変数を行方向に、1変数を列方向に割り当てることにします。まず2行4列の表を作成します(図1)。表の上方向と左方向に、変数の見出しを書く部分も作ります。
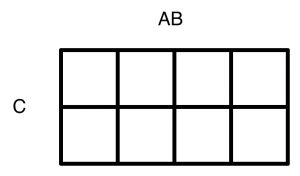
変数の割り当て
変数A,B,Cを行、列に割り当てます。ここでは行方向にAとBを、列方向にCを割り当てます(図2)。割り当てに決まりはありません。行方向にAとCを、列方向にBを割り当てても最終的な結果は同じです。(図2のA,B,Cは実際には書きません。)
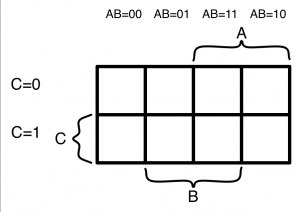
変数の見出しを考える
変数A,B,Cが取り得る値を行、列に割り当てます。行方向はAとBの2変数の組み合わせになります。ここで注意することは、隣同士のセルはAとBの変化を1箇所だけにすることです(Grayコード)。具体的には、00→01→11→10と変化するように見出しを考える必要があります。00→01→10→11と変化させると、01→10の部分で2箇所の値が変化しているので、ベイチ図が機能しなくなります。
列方向のCは1変数なので0と1を割り当てます。次に、表の上下左右に中かっこと変数名を書きます。変数名を書く場所は、その変数の1を割り当てた箇所になります。
セルに値を書き込む
ベイチ図を作成する論理式は主加法標準形で書かれているので、論理式の各項の組み合わせに対応するセルに1を書きます。これでベイチ図は完成です。
$$ Z = \overline{A} \ \overline{B} \ \overline{C} + \overline{A} \ \overline{B} C + AB\overline{C} + A \overline{B} \ \overline{C} + A\overline{B}C \ \ \ \ \ \text{(1)}$$
論理式の最適化
ここから、回路の最適化を行います。ベイチ図で1が連続している部分に注目し、○で囲みます。○で囲む時のルールは次の通りです。
- 1の部分を○で囲む
- 囲んだ中はすべて1になっていること
- 囲んだ表のセルは縦と横かを2のべき乗にする
- 囲みはできるだけ大きくする
- 表の上下、左右の両端はつながっている
- セルは何度囲んでもよい(囲みが重なってもよい)
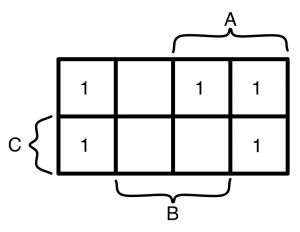
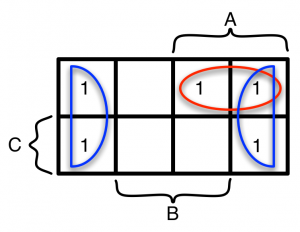
“表の上下、左右の両端はつながっている”は、上下と左右は端がなく、リング状につながっていることを意味します。具体的には図5のAB=10の右端は、左端AB=00につながっていると考えます(左右はメルカトル図法の世界地図のようにつながっている)。また、C=1の下側は上側のC=0につながっていると考えます。
ルールに従って1の部分をできるだけ大きく囲むと、図5のように2つの囲み(赤と青)ができます。
まず、赤い囲みに着目します。この部分だけの論理式を主加法標準形で作成すると式(2)になります。
$$ z1 = AB \ \overline{C} + A \overline{B} \ \overline{C} = A \ \overline{C} ( B + \overline{B} )\ \ \ \ \ \text{(2)}$$
ブール代数より、式(2)の\((B + \overline{B})\)部分は1になります。これは、Bの値が0でも1でも結果は1になるということを意味します。つまり、Bはあってもなくてもどちらでもよいので冗長です。このことから、結局赤い囲みは式(3)になります。
$$ z1 = A \ \overline{C}\ \ \ \ \ \text{(3)} $$
次に青い囲みに着目します。この部分だけの論理式を主加法標準形で作成すると式(4)になります。
\begin{equation}
\begin{split}
z2 &= \overline{A} \ \overline{B} \ \overline{C} + \overline{A} \ \overline{B} \ C + A \overline{B} \ \overline{C} + A \overline{B} \ C \ \ \ \ \ \text{(4)}\\
&= \overline{B} ( \overline{A} \ \overline{C} + \overline{A} C + A \overline{C} + AC) \\
&= \overline{B} ( \overline{A} ( \overline{C} + C ) + A( \overline{C} + C )) \\
&= \overline{B} ( \overline{A} + A) \\
&= \overline{B}
\end{split}
\end{equation}
実際には、このような論理式の展開を行わなくても、図5の青い囲みで0と1の両方が入ってる変数を冗長と考えれば \( z2 = \overline{B} \)ということがわかります。
z1とz2の結果から、最終的な論理式は主加法標準形で次のようになります。
$$ Z = z1 + z2 = A \ \overline{C} + \overline{B} \ \ \ \ \ \text{(5)}$$