主加法標準形の論理式
$$ Z = B + A \bullet C $$
の主乗法標準形を求めます。手順としては、まずカルノー図(またはベイチ図)を作成し、それを参考に主乗法標準形の論理式を求めます。
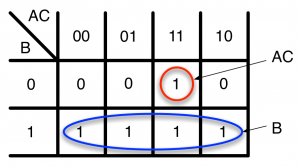
カルノー図の作成
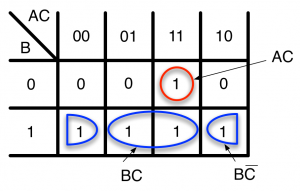
\( Z = B + A \bullet C \)のカルノー図は次のようになります。
カルノー図
主乗法標準形で論理式を作成
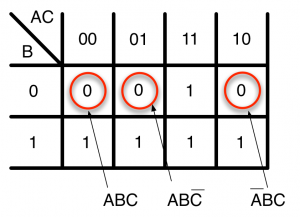
カルノー図で0になっているセルに注目し、主乗法標準形の論理式を作成します。
0のセルに注目
$$ Z = (A+B+C)(A+B+\bar{C})(\bar{A}+B+C) $$
カルノー図から別の主加法標準形の論理式を作成する
\( Z = B + A \bullet C \)は最適化された論理式ですが、Bの項をあえてAを含む冗長な論理に変更します。
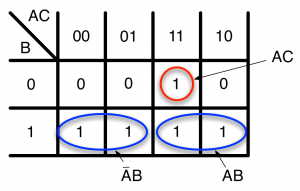
具体的には、カルノー図で4つのセルを囲んでいる青色の部分を、2つの囲みに分割します。その場合、2通りの分割が考えられます。
分割その1
Bの囲みの分割その1
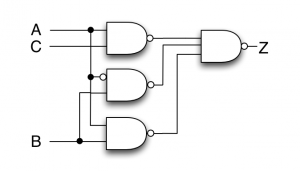
$$ Z = B + AC = \bar{A}B + AB + AC $$
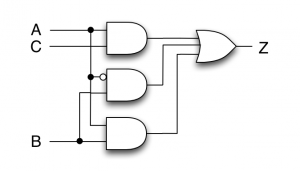
主加法標準形の論理式をそのまま回路図で表すと、次のようになります。
ANDゲートとORゲートで構成
ORが負論理のANDと同じであることを利用すると、次のようにNANDゲートだけで表すこともできます。
NANDゲートで構成
分割その2
Bの囲みの分割その2
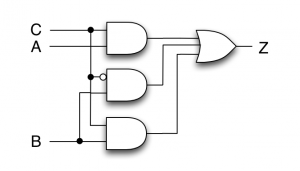
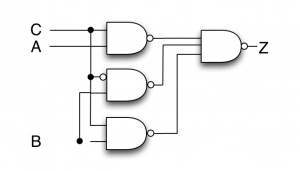
$$ Z = B + AC = BC + B \bar{C} + AC $$
主加法標準形の論理式をそのまま回路図で表すと、次のようになります。
ANDゲートとORゲートで構成
ORが負論理のANDと同じであることを利用すると、次のように表すこともできます。
NANDゲートで構成
